题目内容
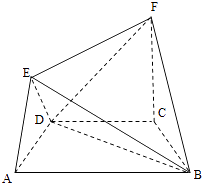
【题目】如图，在等腰三角形ABC中，已知AB=AC=1，A=120°，E，F分别是边AB，AC上的点，且 
， 
，其中m，n∈（0，1）．若EF，BC的中点分别为M，N，且m+4n=1，则 
的最小值为 ．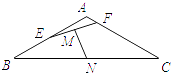 
【答案】
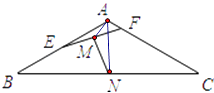
【解析】解：连接AM、AN， ∵等腰三角形ABC中，AB=AC=1，A=120°，
∴ 
=| || 
|cos120°=﹣ 
∵AM是△AEF的中线，
∴ 
= （ 
）= （ 
+ 
）
同理，可得 
= （ + ），
由此可得 
= ﹣ = （1﹣m） + （1﹣n）
∴ 
=[ （1﹣m） + （1﹣n） ]2= 
（1﹣m）2+ （1﹣m）（1﹣n） + （1﹣n）2
= （1﹣m）2﹣ （1﹣m）（1﹣n）+ （1﹣n）2 ，
∵m+4n=1，可得1﹣m=4n
∴代入上式得 = ×（4n）2﹣ ×4n（1﹣n）+ （1﹣n）2= 
n2﹣ 
n+
∵m，n∈（0，1），
∴当n= 
时， 的最小值为 ，此时 
的最小值为 ．
所以答案是： 
练习册系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
