题目内容
设函数 在
在 处取得极值,且曲线
处取得极值,且曲线 在点
在点 处的切线垂直于直线
处的切线垂直于直线 .
.
(1)求 的值;
的值;
(2)若函数 ,讨论
,讨论 的单调性.
的单调性.
【答案】
(1)a=1,b=0;(2)见解析.
【解析】
试题分析:(1)根据极值点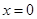 ,求导后可得
,求导后可得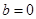 ,由在点
,由在点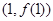 处的切线垂直于直线
处的切线垂直于直线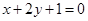 可知该切线斜率为2.可得
可知该切线斜率为2.可得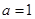 ;(2)对
;(2)对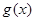 求导后对
求导后对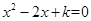 的根的情况进行分类讨论即可.
的根的情况进行分类讨论即可.
试题解析:(1)因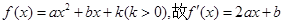 ,又
,又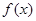 在x=0处取得极限值,故
在x=0处取得极限值,故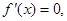 从而
从而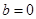 ,由曲线y=
,由曲线y=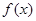 在
在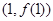 处的切线与直线
处的切线与直线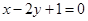 相互垂直可知该切线斜率为2,即
相互垂直可知该切线斜率为2,即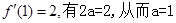 .
.
(2)由(Ⅰ)知,
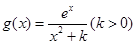 ,
,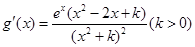 .
.
令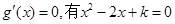 .
.
①当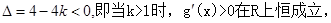
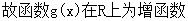 ;
;
②当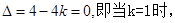
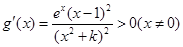 ,g(x)在R上为增函数;
,g(x)在R上为增函数;
③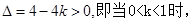 方程
方程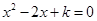 有两个不相等实根,
有两个不相等实根,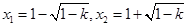
当 函数;
函数;
当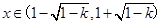 时,
时,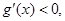 故
故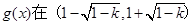 上为减函数;
上为减函数;
当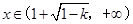 时,
时,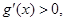 故
故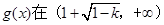 上为增函数.
上为增函数.
考点:1.导数在切线中的运用;2.导数求函数的单调性;3.分类讨论思想的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 且
且
 的代数式表示
的代数式表示 ;
; 的单调区间;
的单调区间;  ,设函数
,设函数 处取得极值,记点
处取得极值,记点 ,证明:线段
,证明:线段 与曲线
与曲线 、
、 的公共点;
的公共点; 在
在 处取得极值,且曲线
处取得极值,且曲线 在点
在点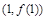 处的切线垂直于直线
处的切线垂直于直线 ,则
,则 的值为 .
的值为 .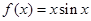 在
在 处取得极值,则
处取得极值,则 的值为()
的值为()
 在
在 处取得极值,则
处取得极值,则 的值为( )
的值为( ) B.
B. C.
C. D.4
D.4