题目内容
设函数 在
在 处取得极值,且曲线
处取得极值,且曲线 在点
在点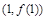 处的切线垂直于直线
处的切线垂直于直线 ,则
,则 的值为 .
的值为 .
【答案】
1
【解析】
试题分析:因f(x)=ax2+bx+k(k>0),故f'(x)=2ax+b又f(x)在x=0处取得极值,故f'(x)=0,从而b=0由曲线y=f(x)在(1,f(1))处的切线与直线x+2y+1=0相互垂直可知
该切线斜率为2,即f'(1)=2,有2a=2,从而a=1,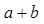 =1.
=1.
考点:本题主要考查待定系数法,导数的几何意义,直线垂直的条件。
点评:中档题,本题具有一定综合性,较全面的考查了待定系数法,导数的几何意义,直线垂直的条件。曲线的切线斜率等于,在切点处的导函数值。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 且
且
 的代数式表示
的代数式表示 ;
; 的单调区间;
的单调区间;  ,设函数
,设函数 处取得极值,记点
处取得极值,记点 ,证明:线段
,证明:线段 与曲线
与曲线 、
、 的公共点;
的公共点;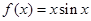 在
在 处取得极值,则
处取得极值,则 的值为()
的值为()
 在
在 处取得极值,则
处取得极值,则 的值为( )
的值为( ) B.
B. C.
C. D.4
D.4