题目内容
设函数
在
处取得极值，则
的值为（ ）
A． 
B．
C．
D．4
【答案】
A.
【解析】因为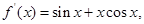
，所以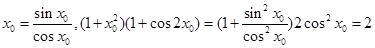
。
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
相关题目
世纪百通主体课堂小学课时同步达标系列答案世纪百通优练测系列答案题目内容
设函数在处取得极值，则的值为（ ）
A． B． C．
D．4
A.
【解析】因为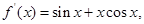，所以。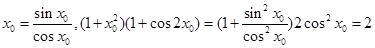
世纪百通主体课堂小学课时同步达标系列答案世纪百通优练测系列答案
,且
的代数式表示b,并求
的单调区间；
,设函数
处取得极值，记点M (
,
)，N(
,
)，P(
), 
,请仔细观察曲线
(
)，线段MP与曲线f(x)均有异于M,P的公共点，试确定t的最小值，并证明你的结论；
n< m,使得线段PQ与曲线f(x)有异于P、Q的公共点，请直接写出m的取值范围（不必给出求解过程） 
且
的代数式表示
；
的单调区间； 
，设函数
处取得极值，记点
，证明：线段
与曲线
、
的公共点；
在
处取得极值，且曲线
在点
处的切线垂直于直线
，则
的值为 .
在
处取得极值，则
的值为（）