题目内容
17.函数$y=\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$的最小值是$\frac{5}{2}$.设x、y∈R+且$\frac{1}{x}$+$\frac{9}{y}$=1,则x+y的最小值为16.分析 换元,利用函数的单调性求出函数$y=\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$的最小值;利用“1”的代换,结合基本不等式,求出x+y的最小值.
解答 解:设$\sqrt{{x}^{2}+2}$=t(t≥2),则y=t+$\frac{1}{t}$在[2,+∞)上是单调增函数,
∴当t=2时,函数的最小值为$\frac{5}{2}$;
∵$\frac{1}{x}$+$\frac{9}{y}$=1,x、y∈R+,
∴x+y=(x+y)•($\frac{1}{x}$+$\frac{9}{y}$)=10+$\frac{y}{x}+\frac{9x}{y}$≥10+2$\sqrt{\frac{y}{x}•\frac{9x}{y}}$=16(当且仅当$\frac{y}{x}=\frac{9x}{y}$,x=4,y=12时取“=”)
∴x+y的最小值为16.
故答案为:$\frac{5}{2}$;16.
点评 本题考查函数的最小值,考查函数的单调性,考查基本不等式的运用,选择正确的方法是关键.

练习册系列答案
相关题目
8.曲线y=lnx-2x在点(1,-2)处的切线与坐标轴所围成的三角形的面积是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | 2 |
2.等差数列{an}中,已知a1+a4+a7=39,a3+a6+a9=27,求a2+a8=( )
| A. | 11 | B. | 22 | C. | 33 | D. | 44 |
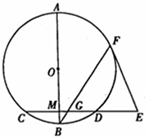 如图,AB是圆O的直径,弦CD⊥AB于点M,E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于G.
如图,AB是圆O的直径,弦CD⊥AB于点M,E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于G.