Question

7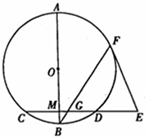．如图，AB是圆O的直径，弦CD⊥AB于点M，E是CD延长线上一点，AB=10，CD=8，3ED=4OM，EF切圆O于F，BF交CD于G．
（1）求证：△EFG为等腰三角形；
（2）求线段MG的长．

Answer 1

分析 （1）连接AF，OF，则A，F，G，M共圆，∠FGE=∠BAF，证明∠EFG=∠FGE，即可证明：△EFG为等腰三角形；
（2）求出EF=EG=4$\sqrt{3}$，连接AD，则∠BAD=∠BFD，即可求线段MG的长．

解答 （1）证明：连接AF，OF，则A，F，G，M共圆，∴∠FGE=∠BAF
∵EF⊥OF，
∴∠EFG=∠BAF，
∴∠EFG=∠FGE
∴EF=EG，
∴△EFG为等腰三角形；
（2）解：由AB=10，CD=8可得OM=3，
∴ED=$\frac{4}{3}$OM=4EF²=ED•EC=48，
∴EF=EG=4$\sqrt{3}$，
连接AD，则∠BAD=∠BFD，
∴MG=EM-EG=8-4$\sqrt{3}$．

点评 本题考查圆的内接四边形的性质，考查学生分析解决问题的能力，属于中档题．