题目内容
已知二次函数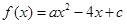 ,且
,且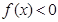 的解集是(1,5).
的解集是(1,5).
(l)求实数a,c的值;
(2)求函数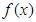 在
在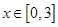 上的值域.
上的值域.
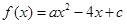 ,且
,且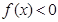 的解集是(1,5).
的解集是(1,5).(l)求实数a,c的值;
(2)求函数
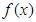 在
在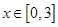 上的值域.
上的值域.(1)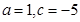 ;(2)
;(2)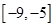 .
.
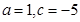 ;(2)
;(2)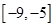 .
.试题分析:(1)不等式的解集对应的区间端点值即是对应方程的根,设
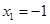 和
和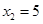 ,根据根与系数的关系找到
,根据根与系数的关系找到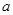 和
和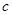 的两个关系式,求解即可;(2)先根据(1)中的结果,利用配方法将函数
的两个关系式,求解即可;(2)先根据(1)中的结果,利用配方法将函数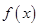 的解析式化简为:
的解析式化简为: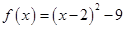 ,结合二次函数的图像与性质可知,函数
,结合二次函数的图像与性质可知,函数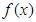 在
在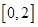 上为减函数,在
上为减函数,在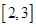 上为增函数,则函数
上为增函数,则函数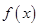 的极小值是
的极小值是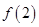 ,然后比较一下区间端点值
,然后比较一下区间端点值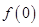 和
和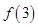 ,函数
,函数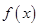 的极小值取两者中的最大值,写出函数
的极小值取两者中的最大值,写出函数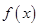 在区间
在区间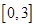 上的值域即可.
上的值域即可.试题解析:(1)由
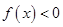 ,得:
,得: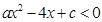 ,不等式
,不等式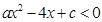 的解集是
的解集是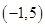 ,
,故方程
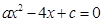 的两根是
的两根是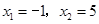 , 3分
, 3分所以
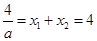 ,
,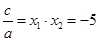 ,
,所以
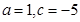 . 6分
. 6分(2)由(1)知,
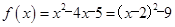 .
.∵
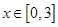 ,∴
,∴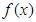 在
在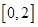 上为减函数,在
上为减函数,在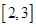 上为增函数.
上为增函数.∴当
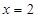 时,
时,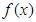 取得最小值为
取得最小值为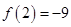 .
.而当
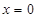 时,
时,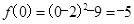 ,当
,当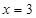 时,
时,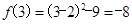 .
. ∴
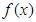 在
在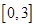 上取得最大值为
上取得最大值为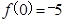 ,
,∴函数
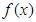 在
在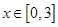 上的值域为
上的值域为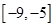 . 12分
. 12分
练习册系列答案
相关题目
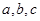 为正实数且满足
为正实数且满足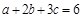 .
.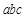 的最大值为
的最大值为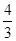 ;(2)求
;(2)求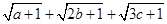 的最大值.
的最大值.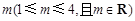 个单位的药剂,它在水中释放的浓度
个单位的药剂,它在水中释放的浓度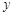 (克/升)随着时间
(克/升)随着时间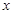 (天)变化的函数关系式近似为
(天)变化的函数关系式近似为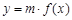 ,其中
,其中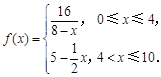 若多次投放,则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
若多次投放,则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.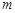 个单位的药剂,要使接下来的4天中能够持续有效治污,试求
个单位的药剂,要使接下来的4天中能够持续有效治污,试求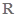 上的单调函数
上的单调函数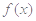 满足
满足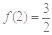 ,且对任意
,且对任意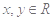 都有
都有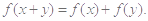
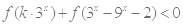 对任意
对任意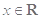 恒成立,求实数
恒成立,求实数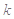 的取值范围.
的取值范围. ,
, .
. 的图象与
的图象与 轴无交点,求
轴无交点,求 的取值范围;
的取值范围; 上存在零点,求
上存在零点,求 ,
, .当
.当 时,若对任意的
时,若对任意的 ,总存在
,总存在 ,使得
,使得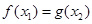 ,求
,求 的取值范围.
的取值范围.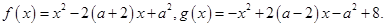 设
设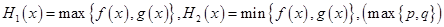 表示
表示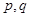 中的较大值,
中的较大值,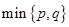 表示
表示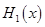 的最小值为
的最小值为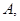
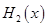 的最大值为
的最大值为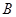 ,则
,则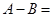 ( )
( )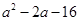
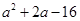
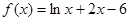 的零点所在的区间为( )
的零点所在的区间为( )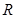 上的函数
上的函数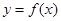 是奇函数,且满足
是奇函数,且满足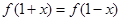 .当
.当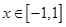 时,
时,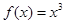 ,则
,则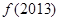 的值是( )
的值是( )