题目内容
((12分)
设函数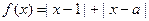
⑴若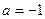 时,解不等式
时,解不等式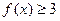 ;
;
⑵如果对于任意的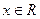 ,
,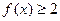 ,求
,求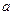 的取值范围。
的取值范围。
设函数
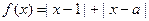
⑴若
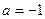 时,解不等式
时,解不等式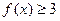 ;
;⑵如果对于任意的
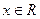 ,
,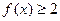 ,求
,求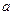 的取值范围。
的取值范围。解:⑴因为函数
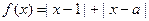 ,所以
,所以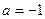 时不等式
时不等式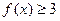
即
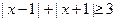 ,由绝对值的几何意义易知解为
,由绝对值的几何意义易知解为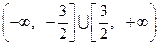 。
。⑵因为对任意的
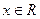 都有
都有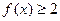 ,即需对任意的
,即需对任意的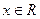 都有
都有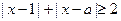
也就是需要
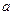
 与
与 之间距离
之间距离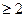 ,所以
,所以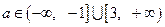 即可
即可所以
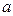 的取值范围是
的取值范围是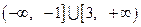 。
。略

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
题目内容
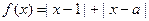
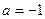 时,解不等式
时,解不等式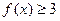 ;
;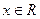 ,
,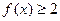 ,求
,求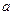 的取值范围。
的取值范围。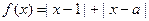 ,所以
,所以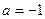 时不等式
时不等式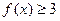
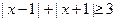 ,由绝对值的几何意义易知解为
,由绝对值的几何意义易知解为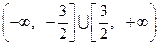 。
。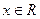 都有
都有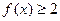 ,即需对任意的
,即需对任意的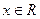 都有
都有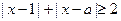
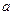
 与
与 之间距离
之间距离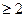 ,所以
,所以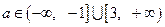 即可
即可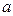 的取值范围是
的取值范围是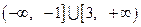 。
。
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案