题目内容
设二次函数f(x)=(k-4)x2+kx(k∈R),对任意实数x,有f(x)≤6x+2恒成立;数列{an}满足an+1=f(an).
(1)求函数f(x)的解析式;
(2)试写出一个区间(a,b),使得当an∈(a,b)时,an+1∈(a,b)且数列{an}是递增数列,并说明理由;
(3)已知a1=![]() ,是否存在非零整数λ,使得对任意n∈N*,都有
,是否存在非零整数λ,使得对任意n∈N*,都有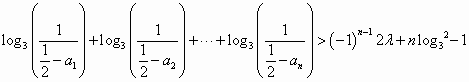 -1+(-1)n-12λ+nlog32恒成立,若存在,求之;若不存在,说明理由.
-1+(-1)n-12λ+nlog32恒成立,若存在,求之;若不存在,说明理由.
答案:
解析:
解析:
|
解:(1)由 从而得:,化简得 所以 (2)解:若数列 又当 所以有 注:本题的区间也可以是 (3)由(2)知 即 令 从而有 从而得 所以 所以 所以, 即 ①当 ②当 所以,对任意 |

练习册系列答案
相关题目
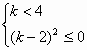 ,从而得
,从而得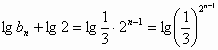 ,即
,即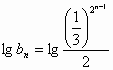 ,
,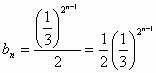 , 10分
, 10分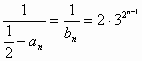 ,所以
,所以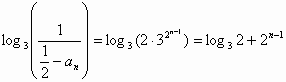 ,
,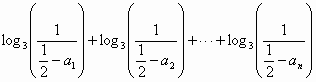
 R,且x+y+z=1,求证x2+y2+z2≥
R,且x+y+z=1,求证x2+y2+z2≥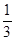 ;
; ,若x
,若x