题目内容
设二次函数f(x)＝x2＋2x＋b的图象与两坐标轴有三个交点，经过这三个交点的圆记为圆C．
(1)求实数b的取值范围；
(2)求圆C的方程；
(3)问圆C是否经过某定点(其坐标与b无关)？若是，求出定点的坐标；若不是，说明理由．
答案：
解析：
解析：
|
解：(1)令x＝0，得抛物线与y轴交点是(0，b)．因为f(x)的图象与两坐标轴有三个交点，所以b≠0．令f(x)＝x2＋2x＋b＝0，则Δ＝4－4b＞0，解得b＜1．所以b的取值范围是(－∞，0)∪(0，1)． (2)设圆C的方程为x2＋y2＋Dx＋Ey＋F＝0．令y＝0，得x2＋Dx＋F＝0．由题意知，该方程与x2＋2x＋b＝0的根相同，故D＝2，F＝b．令x＝0，得y2＋Ey＋F＝0．由题意知，此方程有一个根为b，代入得E＝－b－1．所以圆C的方程为x2＋y2＋2x－(b＋1)y＋b＝0． (3)将圆C的方程变形为(1－y)b＋(x2＋y2＋2x－y)＝0．由于b的任意性，得 |
解得
．所以圆C必过定点(0，1)和(－2，1)．
练习册系列答案
相关题目
R，且x＋y＋z＝1，求证x2＋y2＋z2≥
；
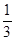，若x
． 