题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
在(2)中令x=1,有1≤f(1)≤1,故f(1)=1 3分 |
(2) |
由(1)知二次函数的关于直线x=-1对称,且开口向上 故设此二次函数为f(x)=a(x+1)2,(a>0),∵f(1)=1,∴a= ∴f(x)= |
(3) |
f(x+t)≤x 令g(x)=x2+(2t-2)x+t2+2t+1,g(x)≤0,x∈[1,3].
∴tmax=-4+2 |

练习册系列答案
相关题目
| |||||||||||
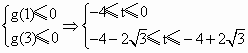 ∴-4≤t≤-4+2
∴-4≤t≤-4+2