题目内容
设二次函数f(x)=ax2+bx+c(a>0),方程f(x)-x=0的两根x1、x2满足0<x1<x2<(1)当x∈(0,x1)时,证明x<f(x)<x1;
(2)设函数f(x)的图象关于直线x=x0对称;
证明:x0<![]()
解:
(1)令F(x)=f(x)-x,由x1、x2是方程f(x)-x=0的两根,有F(x)=a(x-x1)(x-x2)
当x∈(0,x1)时,由x1≤x2,及a>0,有F(x)=a(x-x1)(x-x2)>0,?
即F(x)=f(x)-x>0,f(x)>x.?
又x1-f(x)=x1-[x+F(x)]=x1-x-a(x-x1)(x-x2)=(x1-x)[1+a(x-x2)]
因为0<x<x1<x2<![]()
所以x1-x>0,1+a(x-x2)=1+ax-ax2>1-ax2>0
得x1>f(x),所以x<f(x)<x1;?
(2)依题意x0=-![]() ,因x1、x2是f(x)-x=0的根,即x1、x2是方程ax2+(b-1)x+c=0的根.
,因x1、x2是f(x)-x=0的根,即x1、x2是方程ax2+(b-1)x+c=0的根.
所以x1+x2=-![]() ,
,
x0=-![]() =
=![]() =
=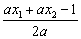
因为ax2<1,即ax2-1<0,故x0=![]() <
<![]() =
=![]() .
.
评述:此题考查一元二次方程、二次函数和不等式的基础知识,考查综合运用数学知识分析问题和解决问题的能力.考查证明不等式的方法.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
 R,且x+y+z=1,求证x2+y2+z2≥
R,且x+y+z=1,求证x2+y2+z2≥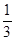 ;
; ,若x
,若x