题目内容
2.已知平面图形ABCD为凸四边形(凸四边形即任取平面四边形一边所在的直线,其余各边均在此直线的同侧),且AB=2,BC=4,CD=5,DA=3,则四边形ABCD面积S的最大值为( )| A. | $\sqrt{30}$ | B. | 2$\sqrt{30}$ | C. | 4$\sqrt{30}$ | D. | 6$\sqrt{30}$ |
分析 设AC=x,在△ABC和△ACD中,由余弦定理可得,15cosD-8cosB=7,再由三角形的面积公式可得8sinB+15sinD=2S,两式两边平方结合两角和的余弦公式和余弦函数的值域,即可求得最大值.
解答 解:设AC=x,在△ABC中,由余弦定理可得,
x2=22+42-2×2×4cosB=20-16cosB,
在△ACD中,由余弦定理可得,
x2=32+52-2×3×5cosD=34-30cosD,
即有15cosD-8cosB=7,
又四边形ABCD面积S=$\frac{1}{2}$×2×4sinB+$\frac{1}{2}$×3×5sinD
=$\frac{1}{2}$(8sinB+15sinD),
即有8sinB+15sinD=2S,
又15cosD-8cosB=7,
两式两边平方可得,64+225+240(sinBsinD-cosBcosD)=49+4s2,
化简可得,-240cos(B+D)=4S2-240,
由于-1≤cos(B+D)<1,即有S≤2$\sqrt{30}$.
当cos(B+D)=-1即B+D=π时,4S2-240=240,
解得S=2$\sqrt{30}$.
故S的最大值为2$\sqrt{30}$.
故选B.
点评 本题考查三角形的面积公式和余弦定理的运用,同时考查两角和的余弦公式的运用和余弦函数的最值的求法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10. 一个算法的程序框图如图所示,若输入的x值为2015,则输出的i值为( )
一个算法的程序框图如图所示,若输入的x值为2015,则输出的i值为( )
 一个算法的程序框图如图所示,若输入的x值为2015,则输出的i值为( )
一个算法的程序框图如图所示,若输入的x值为2015,则输出的i值为( )| A. | 3 | B. | 5 | C. | 6 | D. | 9 |
14.设f(x)=x2+2cosx,x∈R,且f(α)>f(β),则下列结论中成立的是( )
| A. | α>β | B. | α2<β2 | C. | α<β | D. | α2>β2 |
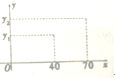 行驶中的 汽车在刹车时,由于惯性作用,要继续向前滑行一段距离才能停下来,这断距离叫做刹车距离,某种路面上,某种型号汽车的刹车距离ym与汽车的车速xkm/h满足下列关系:y=$\frac{nx}{100}$+$\frac{{x}^{2}}{400}$(n为常数,n∈N),做两次刹车实验,有数据如图,其中5<y1<7,13<y2<15
行驶中的 汽车在刹车时,由于惯性作用,要继续向前滑行一段距离才能停下来,这断距离叫做刹车距离,某种路面上,某种型号汽车的刹车距离ym与汽车的车速xkm/h满足下列关系:y=$\frac{nx}{100}$+$\frac{{x}^{2}}{400}$(n为常数,n∈N),做两次刹车实验,有数据如图,其中5<y1<7,13<y2<15