题目内容
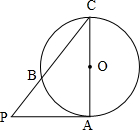已知PA是圆O的切线，切点为A，PA=2．AC是圆O的直径，PC与圆O交于点B，PB=1，则圆O的半径R=分析：连接AB，根据弦切角定理及三角形相似的判定，我们易得△PBA～△PAC，再由相似三角形的性质，我们可以建立未知量与已知量之间的关系式，解方程即可求解．
解答：解：依题意，我们知道△PBA～△PAC，
由相似三角形的对应边成比例性质我们有
=
，
即R=
=
=
．
故答案为：
．
由相似三角形的对应边成比例性质我们有
| PA |
| 2R |
| PB |
| AB |
即R=
| PA•AB |
| 2PB |
2×
| ||
| 2×1 |
| 3 |
故答案为：
| 3 |
点评：在平面几何中，我们要求线段的长度，关键是寻找未知量与已知量之间的关系，寻找相似三角形和全等三角形是常用的方法，根据相似三角形的性质，很容易得到已知量与未知量之间的关系，解方程即可求解．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知PA是圆O的切线，切点为A，PO交圆O于B，C两点，
如图，已知PA是圆O的切线，切点为A，AC是圆O的直径，PC与圆O交于点B，PA=4，圆O的半径是
（几何证明选讲选做题）
A．（坐标系与参数方程选做题）在极坐标系中，点