题目内容
函数 是( )
是( )
| A.偶函数 | B.既是奇函数又是偶函数 |
| C.奇函数 | D.非奇非偶函数函数 |
C
解析试题分析:因为f(-x)= -f(x),所以选C。
考点:本题主要考查简单函数的奇偶性。
点评:简单题,判断函数的奇偶性,首先应看函数的定义域是否关于原点对称,然后研究f(x)与f(-x)的关系。

练习册系列答案
相关题目
已知 ,且
,且 为奇函数,若
为奇函数,若 ,则
,则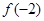 的值为
的值为
A. | B. | C. | D. |
函数 的图象如右图所示,下列说法正确的是( )
的图象如右图所示,下列说法正确的是( )
①函数 满足
满足
②函数 满足
满足
③函数 满足
满足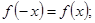
④函数 满足
满足

| A.①③ | B.②④ | C.①② | D.③④ |
函数 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A. | B. | C. | D. |
定义域是一切实数的函数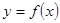 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数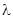 (
(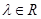 )使得
)使得  对任意实数
对任意实数 都成立,则称
都成立,则称 是一个“
是一个“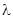 —伴随函数”.有下列关于“
—伴随函数”.有下列关于“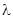 —伴随函数”的结论:
—伴随函数”的结论:
① 是常数函数中唯一一个“
是常数函数中唯一一个“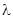 —伴随函数”;
—伴随函数”;
②“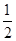 —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;
③ 是一个“
是一个“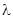 —伴随函数”;
—伴随函数”;
其中正确结论的个数是 ( )
| A.1个; | B.2个; | C.3个; | D.0个; |
已知 ,若函数
,若函数 ,则
,则 的
的
根的个数最多有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知函数 是
是 上的偶函数,若对于
上的偶函数,若对于 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D.1 |
下列四组函数中,表示相同函数的一组是( )
A. | B. |
C. | D. |
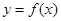 在区间
在区间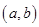 的导函数为
的导函数为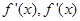 在区间
在区间 若在区间
若在区间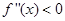 恒成立,则称函数
恒成立,则称函数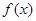 在区间
在区间 ,若对任意的实数m满足
,若对任意的实数m满足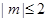 时,函数
时,函数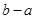 的最大值为( )
的最大值为( )