题目内容
已知函数 是
是 上的偶函数,若对于
上的偶函数,若对于 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D.1 |
C
解析试题分析:∵函数f(x)是(-∞,+∞)上的偶函数,
∴f(-x)=f(x),
又∵对于x≥0都有f(x+2)=-f(x),∴f(x+4)=-f(x+2)=f(x)
∴T=4,∵当x∈[0,2)时,f(x)=log2(x+1),
∴f(-2011)+f(2012)=f(2011)+f(2012)=f(4×502+3)+f(4×503)
=f(3)+f(0)=-f(1)+f(0)=-log22+log21=-1,
故选C.
考点:本题主要考查函数的奇偶性及周期性,对数函数的性质。
点评:小综合题,首先根据f(x)是(-∞,+∞)上的偶函数,可得f(-x)=f(x),知f(-2011)=f(2011),求出函数的周期T=4,利用当x∈[0,2)时,f(x)=log2(x+1)的解析式,进行求解.

练习册系列答案
相关题目
函数 的值域是( )
的值域是( )
A. | B. | C. | D. |
函数 是( )
是( )
| A.偶函数 | B.既是奇函数又是偶函数 |
| C.奇函数 | D.非奇非偶函数函数 |
已知 ,则在下列区间中,
,则在下列区间中,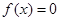 有实数解的是( ).
有实数解的是( ).
| A.(-3,-2) | B.(-1,0) | C.(2,3) | D.(4,5) |
若函数 满足
满足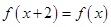 且
且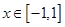 时,
时,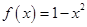 ,函数
,函数 ,则函数
,则函数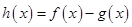 在区间
在区间 内的零点的个数为( )
内的零点的个数为( )
A. | B. | C. | D. |
已知函数 的图象如图所示(其中
的图象如图所示(其中 是函数
是函数 的导函数).下面四个图象中,
的导函数).下面四个图象中,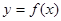 的图象大致是( )
的图象大致是( )

| A. | B. | C. | D. |
函数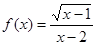 的定义域为( )
的定义域为( )
| A.[1,2)∪(2,+∞) | B.(1,+∞) | C.[1, 2) | D.[2,+∞) |
根据表格中的数据,可以判断方程 必有一个根在区间( )
必有一个根在区间( )
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.78 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
B.(0,1)
C.(1,2)
D.(2,3)
 是
是 上的偶函数,满足
上的偶函数,满足 ,当
,当 时,
时,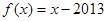 ,则( )
,则( ) B.
B.
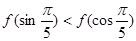 D.
D.