题目内容
函数 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A. | B. | C. | D. |
B
解析试题分析:因为求解函数 的零点所在的区间,只要保证端点值的函数值异号即可,那么由于f(2)=ln2-1<0,f(e)=lne-
的零点所在的区间,只要保证端点值的函数值异号即可,那么由于f(2)=ln2-1<0,f(e)=lne-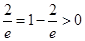 ,且在定义域内连续的函数,则可知选B。而选项A,C,D的端点值函数值同号,舍去。也可以通过函数的单调性可知,函数是定义域上增函数,由于f(2)<0,f(e)>0,可知f(1)<0, f(3)>0,故选B.
,且在定义域内连续的函数,则可知选B。而选项A,C,D的端点值函数值同号,舍去。也可以通过函数的单调性可知,函数是定义域上增函数,由于f(2)<0,f(e)>0,可知f(1)<0, f(3)>0,故选B.
考点:本试题主要是考查了函数的零点的概念,以及基本初等函数的零点所在的区间问题,可以根据判定定理,也可以结合图象与图像来进行,考查了分析问题和解决问题的能力。
点评:确定零点所在的区间,利用零点存在性定理可以逐一分析证明,也可以利用图像与图像的交点问题来分析。同时能注意到函数的单调性,将给判定符号带来方便之处。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
用二分法求 的近似解(精确到0.1),利用计算器得
的近似解(精确到0.1),利用计算器得 ,
, ,则近似解所在区间是( )
,则近似解所在区间是( )
A. | B. |
C. | D. |
函数 的值域是( )
的值域是( )
A. | B. | C. | D. |
函数 是( )
是( )
| A.偶函数 | B.既是奇函数又是偶函数 |
| C.奇函数 | D.非奇非偶函数函数 |
已知 ,则在下列区间中,
,则在下列区间中,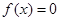 有实数解的是( ).
有实数解的是( ).
| A.(-3,-2) | B.(-1,0) | C.(2,3) | D.(4,5) |
函数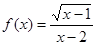 的定义域为( )
的定义域为( )
| A.[1,2)∪(2,+∞) | B.(1,+∞) | C.[1, 2) | D.[2,+∞) |
 的图像向右平移1个单位长度,再向上平移3个单位长度,所得的图像所对应的函数解析式为( )
的图像向右平移1个单位长度,再向上平移3个单位长度,所得的图像所对应的函数解析式为( )



 和函数
和函数 的图象如图所示:则函数
的图象如图所示:则函数 的图象可能是
的图象可能是

 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断: ,则f(P)∩f(M)=
,则f(P)∩f(M)=