题目内容
6．设3＜（$\frac{1}{3}$）x＜27，则正确的是（ ）| A． | {x|-1＜x＜3} | B． | {x|x＜-1或x＞3} | C． | {x|-3＜x＜-1} | D． | {x|1＜x＜3} |
分析 原不等式可化为31＜3-x＜33，由指数函数y=3x的单调性可得．
解答 解：原不等式可化为31＜3-x＜33，
由指数函数y=3x单调递增可得1＜-x＜3，
变形可得-3＜x＜-1，
故选：C．
点评 本题考查指数不等式的解法，涉及指数函数的单调性，属基础题．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
16．若a=20.5，b=0.32.1，c=log${\;}_{\frac{1}{2}}$5，d=log${\;}_{\frac{1}{3}}$5，则（ ）
| A． | b＞a＞c＞d | B． | b＞a＞d＞c | C． | a＞b＞d＞c | D． | a＞b＞c＞d |
17．在△ABC中，A=60°，a=3，则$\frac{a-2b+3c}{sinA-2sinB+3sinC}$=（ ）
| A． | $\frac{8\sqrt{3}}{3}$ | B． | $\frac{2\sqrt{39}}{3}$ | C． | $\frac{26\sqrt{3}}{3}$ | D． | 2$\sqrt{3}$ |
4．第16届亚运会于2010年11月12日至27日在中国广州进行，为了搞好接待工作，组委会招募了 16 名男志愿者和 14名女志愿者，调查发现，男、女志愿者中分别有 10 人和 6 人喜爱运动，其余不喜爱．
（1）根据以上数据完成以下 2×2 列联表：
（2）根据列联表的独立性检验，能否在犯错误的概率不超过0.10 的前提下认为性 别与喜爱运动有关？
参考公式：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中 n=a+b+c+d．
（1）根据以上数据完成以下 2×2 列联表：
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 总计 | 30 |
参考公式：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中 n=a+b+c+d．
| P（ k2≥k0） | 0.40 | 0.25 | 0.10 | 0.05 | 0.010 |
| k0 | 0.708 | 1.323 | 2.706 | 3.841 | 6.635 |
1．以下是程序框图的基本逻辑结构，顺序正确的是（ ）
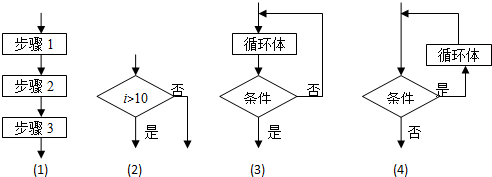
| A． | （1）是顺序结构（2）是条件结构（3）是当型循环结构（4）是直到型循环结构 | |
| B． | （1）是条件结构（2）是顺序结构（3）是当型循环结构（4）是直到型循环结构 | |
| C． | （1）是顺序结构（2）是条件结构（3）是直到型循环结构（4）是当型循环结构 | |
| D． | （1）是顺序结构（2）是当型循环结构（3）是条件结构（4）是直到型循环结构 |
2．对于向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$和实数λ，下列正确的是（ ）
| A． | 若$\overrightarrow{a}$•$\overrightarrow{b}$=0，则$\overrightarrow{a}$=0或$\overrightarrow{b}$=0 | B． | 若λ$\overrightarrow{a}$=0，则λ=0或$\overrightarrow{a}$=$\overrightarrow{0}$ | ||
| C． | 若$\overrightarrow{a}$2=$\overrightarrow{b}$2，则$\overrightarrow{a}$=$\overrightarrow{b}$或$\overrightarrow{a}$=-$\overrightarrow{b}$ | D． | 若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$，则$\overrightarrow{b}$=$\overrightarrow{c}$ |