题目内容
【题目】已知椭圆![]() 的两个焦点是
的两个焦点是![]() ,
, ![]() ,且椭圆
,且椭圆![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过椭圆![]() 的左焦点
的左焦点![]() 且斜率为1的直线
且斜率为1的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求线段
两点,求线段![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)椭圆![]() 的两个焦点是
的两个焦点是![]() ,
, ![]() ,可得
,可得![]() ,椭圆
,椭圆![]() 经过点
经过点![]() 可得
可得![]() ,从而可得椭圆
,从而可得椭圆![]() 的标准方程;(2)直线
的标准方程;(2)直线![]() 的方程为
的方程为![]() ,
,
代入方程![]() 并整理,得
并整理,得![]() ,利用韦达定理和弦长公式计算弦长.
,利用韦达定理和弦长公式计算弦长.
试题解析:(1)由已知得,椭圆![]() 的焦点在
的焦点在![]() 轴上.
轴上.
可设椭圆![]() 的方程为
的方程为![]() ,
,
点![]() 是椭圆
是椭圆![]() 短轴的一个顶点,可得
短轴的一个顶点,可得![]() ,
,
由题意可知![]() ,则有
,则有![]() ,
,
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由已知得,直线![]() 的方程为
的方程为![]() ,
,
代入方程![]() 并整理,得
并整理,得![]() .
.
设![]() ,则
,则![]() ,
,
则![]()
![]() .
.
【方法点晴】本题主要考查待定系数求椭圆方程以、韦达定理及弦长公式,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.

练习册系列答案
相关题目
【题目】在刚刚结束的五市联考中,某校对甲、乙两个文科班的数学成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀,成绩统计后,得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
班级 | 优秀 | 非优秀 | 合计 |
甲班 | 18 | ||
乙班 | 43 | ||
合计 | 110 |
(1)请完成上面的列联表;
(2)请问:是否有![]() 的把握认为“数学成绩与所在的班级有关系”?
的把握认为“数学成绩与所在的班级有关系”?
(3)用分层抽样的方法从甲、乙两个文科班的数学成绩优秀的学生中抽取5名学生进行调研,然后再从这5名学生中随机抽取2名学生进行谈话,求抽到的2名学生中至少有1名乙班学生的概率.
参考公式: 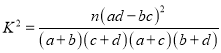 (其中
(其中![]() )
)
参考数据:
|
|
|
|
|
|
|
|
|
|