题目内容
18.若点M是△ABC所在平面内的一点,且满足5$\overrightarrow{AM}$=2$\overrightarrow{AD}$+3$\overrightarrow{AC}$,则△ABM与△ABC的面积比为$\frac{3}{5}$.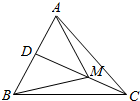
分析 根据题意,求出DM与DC的比值,即可求出△ABM与△ABC的面积比.
解答 解:∵5$\overrightarrow{AM}$=5($\overrightarrow{AD}$+$\overrightarrow{DM}$),
2$\overrightarrow{AD}$+3$\overrightarrow{AC}$=2$\overrightarrow{AD}$+3($\overrightarrow{AD}$+$\overrightarrow{DC}$),
∴5$\overrightarrow{AD}$+5$\overrightarrow{DM}$=5$\overrightarrow{AD}$+3$\overrightarrow{DC}$,
即$\frac{DM}{DC}$=$\frac{3}{5}$;
∴△ABM与△ABC的面积比为
$\frac{\frac{1}{2}•AB{•h}_{1}}{\frac{1}{2}•AB{•h}_{2}}$=$\frac{DM}{DC}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查了平面向量的几何意义以及三角形的面积公式的应用问题,是基础题目.

练习册系列答案
相关题目
8.已知向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(sinα,cosα),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则sinαcosα=( )
| A. | $\frac{12}{25}$ | B. | -$\frac{12}{25}$ | C. | -$\frac{9}{25}$ | D. | $\frac{9}{25}$ |
6.已知函数f(x)=sin(2x-$\frac{π}{6}$),则下面说法正确的是( )
| A. | 函数图象关于点($\frac{π}{12}$,0)对称 | B. | 函数图象的-条对称轴方程为x=$\frac{π}{6}$ | ||
| C. | 函数f(x)是奇函数 | D. | 函数f(x)是偶函数 |
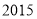 年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取
年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取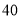 名学生的数学成绩进行统计,将他们的成绩分成六段
名学生的数学成绩进行统计,将他们的成绩分成六段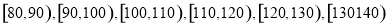 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.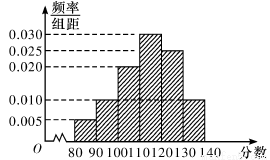
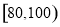 内的学生中任意抽取2人,求成绩在
内的学生中任意抽取2人,求成绩在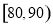 中至少有一人的概率.
中至少有一人的概率. 如图,在△ABC中,G为重心,在AD的延长线上取一点G′,使得GD=G′D=4,若CG=6,BG=10,求△ABC的面积.
如图,在△ABC中,G为重心,在AD的延长线上取一点G′,使得GD=G′D=4,若CG=6,BG=10,求△ABC的面积.