题目内容
10.已知f(x)在(0,+∞)是增函数,又有f(f(x)+$\frac{1}{x}$)=$\frac{1}{f(x)}$,求f(1)分析 根据条件设f(x)=$\frac{k}{x}$,利用待定系数法进行求解即可.
解答 解:根据条件可知f(x)为反比例函数,设f(x)=$\frac{k}{x}$,
∵f(x)在(0,+∞)是增函数,∴k<0,
代入方程得f($\frac{k}{x}$+$\frac{1}{x}$)=f($\frac{k+1}{x}$)=$\frac{x}{k}$,
即$\frac{kx}{k+1}$=$\frac{x}{k}$,
即k2=k+1,即k2-k-1=0,
解得k=$\frac{1-\sqrt{5}}{2}$或k=$\frac{1+\sqrt{5}}{2}$(舍),
即f(x)=$\frac{1-\sqrt{5}}{2x}$,则f(1)=$\frac{1-\sqrt{5}}{2}$.
点评 本题主要考查函数值的计算,根据条件求出函数的解析式是解决本题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
2.已知全集U=R,A={x|-2<x<2},B={x|x2-3x-4≤0},则∁U(A∩B)=( )
| A. | {x|-1≤x<2} | B. | {x|x<-1或x≥2} | C. | {x|-1≤x≤4} | D. | {x|x>4或x<1} |
 ,则
,则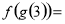 ( )
( )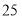 B.
B. 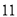 C.
C. 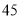 D.
D. 
 如图,在△ABC中,G为重心,在AD的延长线上取一点G′,使得GD=G′D=4,若CG=6,BG=10,求△ABC的面积.
如图,在△ABC中,G为重心,在AD的延长线上取一点G′,使得GD=G′D=4,若CG=6,BG=10,求△ABC的面积.