题目内容
20.函数y=$\frac{x}{lo{g}_{2}(x-1)}$的定义域是{x|x>1,且x≠2}.分析 根据函数的解析式,列出使解析式有意义的不等式组,求出解集即可.
解答 解:∵函数y=$\frac{x}{lo{g}_{2}(x-1)}$,
∴$\left\{\begin{array}{l}{x-1>0}\\{x-1≠1}\end{array}\right.$,
解得x>1,且x≠2,
∴函数y的定义域是{x|x>1,且x≠2}.
故答案为:{x|x>1,且x≠2}.
点评 本题考查了利用函数的解析式求定义域的应用问题,是基础题目.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
9.过椭圆$\frac{{x}^{2}}{4}+{y}^{2}=1$焦点且与椭圆长轴垂直的直线与椭圆相交于A、B两点,则|AB|等于( )
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 1 | D. | 4$\sqrt{3}$ |
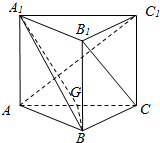 如图,直三棱柱(侧棱与底面垂直的棱柱)ABC-A1B1C1中,点G是AC的中点.
如图,直三棱柱(侧棱与底面垂直的棱柱)ABC-A1B1C1中,点G是AC的中点.