题目内容
已知命题“?x∈R，x2-ax+1＜0”为假命题，则实数a的取值范围是______．
∵命题“存在实数x，使x2-ax+1＜0”的否定是任意实数x，使x2-ax+1≥0，
命题否定是真命题，
∴△=（-a）2-4≤0
∴-2≤a≤2．
实数a的取值范围是：[-2，2]．
故答案为：[-2，2]．
命题否定是真命题，
∴△=（-a）2-4≤0
∴-2≤a≤2．
实数a的取值范围是：[-2，2]．
故答案为：[-2，2]．
练习册系列答案
阅读快车系列答案
相关题目
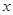公里的相邻两增压站之间的输油管道费用为
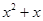万元．设余下工程的总费用为
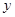万元．
，命题Q：
，那么下列结论不正确的是