题目内容
8.已知函数f(x)=x2+2ax+2.(1)当a=1时,求函数f(x)在区间[-2,3)上的值域;
(2)当a=-1时,求函数f(x)在区间[t,t+1]上的最大值;
(3)求f(x)在[-5,5]上的最大值与最小值.
分析 (1)函数在[-2,-1)上单调递减,在(-1,3]上单调递增,可得函数f(x)在区间[-2,3)上的值域;
(2)当a=-1时,f(x)=x2-2x+2=(x-1)2+1,分类讨论,即可求函数f(x)在区间[t,t+1]上的最大值;
(3)由于二次函数的对称轴为x=-a,分①当-a<-5、②当-5≤-a<0、③当0≤-a≤5、④当-a>5四种情况,分别利用二次函数的性质求得函数的最值.
解答 解:(1)当a=1时,f(x)=x2+2x+2=(x+1)2+1,
函数在[-2,-1)上单调递减,在(-1,3]上单调递增,
∴x=-1,f(x)min=1,x=3,f(x)max=17,
∴函数f(x)在区间[-2,3)上的值域是[1,17];
(2)当a=-1时,f(x)=x2-2x+2=(x-1)2+1,
t$<\frac{1}{2}$,函数f(x)在区间[t,t+1]上的最大值f(t)=(t-1)2+1;
t≥$\frac{1}{2}$,函数f(x)在区间[t,t+1]上的最大值f(t+1)=t2+1;
∴函数f(x)在区间[t,t+1]上的最大值$\left\{\begin{array}{l}{(t-1)^{2}+1,t<\frac{1}{2}}\\{{t}^{2}+1,t≥\frac{1}{2}}\end{array}\right.$;
(3)∵函数f(x)=x2+2ax+2=(x+a)2+2-a2 的对称轴为x=-a,
①当-a<-5,即a>5时,函数y在[-5,5]上是增函数,
当x=-5时,函数y取得最小值为27-10a;当x=5时,函数y取得最大值为27+10a.
②当-5≤-a<0,即0<a≤5时,当x=-a时,函数y取得最小值为2-a2;当x=5时,函数y取得最大值为27+10a.
③当0≤-a≤5,即-5≤a≤0时,x=-a时,函数y取得最小值为2-a2;当x=-5时,函数y取得最大值为27-10a.
④当-a>5,即a<-5时,函数y在[-5,5]上是减函数,故当x=-5时,函数y取得最大值为27-10a;当x=5时,函数y取得最小值为27+10a.
点评 本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了分类讨论的数学思想,属于中档题.

| A. | logba<logab<logb$\frac{b}{a}$ | B. | logb$\frac{b}{a}$<logba<logab | ||
| C. | logba<logb$\frac{b}{a}$<logab | D. | logab<logb$\frac{b}{a}$<logba |
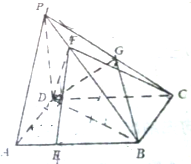 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC的中点,E,F分别为AB,PB上一点,AB=4$\sqrt{2}$,AE=$\sqrt{2}$,PB=4PF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC的中点,E,F分别为AB,PB上一点,AB=4$\sqrt{2}$,AE=$\sqrt{2}$,PB=4PF.