题目内容
8.函数y=2x+log2x-6的零点所在的区间是($\frac{k}{2}$,$\frac{k+1}{2}$),则正整数k的值为4.分析 根据函数零点的判定定理,即可求得结论
解答 解:∵函数f(x)=log2x+2x-6,
∴f′(x)=2+$\frac{1}{xln2}$>0,
∴函数f(x)在(0,+∞)单调递增,
∵f($\frac{3}{2}$)=${log}_{2}^{3}$-4<0,f(3)=log23>0,
∴f($\frac{3}{2}$)•f(3)<0,
且函数f(x)=log2x+2x-6在区间($\frac{3}{2}$,3)上是连续的,
故函数f(x)=log2x+2x-6的零点所在的区间为($\frac{3}{2}$,3),
∴$\left\{\begin{array}{l}{\frac{k}{2}>\frac{3}{2}}\\{\frac{k+1}{2}<3}\end{array}\right.$,解得:3<k<5,
∴k=4,
故答案为:4.
点评 本题主要考查函数零点区间的判断,判断的主要方法是利用根的存在性定理,判断函数在给定区间端点处的符号是否相反.

练习册系列答案
相关题目
16.已知M是△ABC内的一点,且|AB||AC|=4,∠BAC=30°,若△MBC,△MCA,△MAB的面积分别为$\frac{1}{2}$、x、y,则$\frac{1}{x}$+$\frac{4}{y}$的最小值为( )
| A. | 20 | B. | 19 | C. | 18 | D. | 16 |
20.已知α为第二象限角,$sinα+cosα=\frac{1}{5}$,则cos2α=( )
| A. | $-\frac{12}{25}$ | B. | $\frac{7}{5}$ | C. | $\frac{1}{25}$ | D. | $-\frac{7}{25}$ |
17.化简(x-4)4+4(x-4)3+6(x-4)2+4(x-4)+1得( )
| A. | x4 | B. | (x-3)4 | C. | (x+1)4 | D. | x5 |
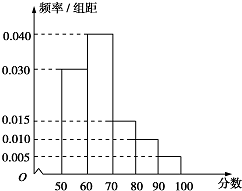 某中学举行电脑知识竞赛,将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,则高一参赛学生成绩的中位数为65.
某中学举行电脑知识竞赛,将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,则高一参赛学生成绩的中位数为65.