题目内容
【题目】函数![]() ,则
,则![]() 在
在![]() 的最大值
的最大值![]() ( )
( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】f′(x)=x![]() 2kx=x(
2kx=x(![]() 2k),
2k),
令f′(x)=0得x=0或x=ln2k,
令g(k)=kln2k,则g′(k)=1![]() <0
<0
∴g(k)在(![]() ,1]上是减函数,∴g(k)g(1)=1ln2>0,
,1]上是减函数,∴g(k)g(1)=1ln2>0,
∴k>ln2k,
∴f(x)在[0,ln2k]上单调递减,在(ln2k,k]上单调递增,
∴f(x)的最大值为f(0)或f(k).
f(k)f(0)=(k1)ekk3+1=(k1)(ekk2k1),
令h(x)=ekk2k1,则h′(k)=ek2k1,h′′(k)=ek2,
令h″(k)=0得k=ln2,
∴h′(k)在(![]() ,ln2)上单调递减,在(ln2,1]上单调递增,
,ln2)上单调递减,在(ln2,1]上单调递增,
∵h′(![]() )=
)=![]() 2<0,h′(1)=e3<0,
2<0,h′(1)=e3<0,
∴h′(k)<0在(![]() ,1]上恒成立,
,1]上恒成立,
∴h(k)在(![]() ,1]上是减函数,∴h(k)<h(
,1]上是减函数,∴h(k)<h(![]() )=
)=![]()
![]() <0,
<0,
∴f(k)f(0),
∴f(x)的最大值为f(k)=(k1)ekk3,
故选D.
方法 | 步骤 |
单调性法 | 先确定函数的单调性,再由单调性求最值 |
图象法 | 先作出函数的图象,再观察其最高点、最低点,求出最值 |
基本不等式法 | 先对解析式变形,使之具备“一正二定三相等”的条件后用基本不等式求出最值 |
导数法 | 先求导,然后求出在给定区间上的极值,最后结合端点值,求出最值 |
换元法 | 对比较复杂的函数可通过换元转化为熟悉的函数,再用相应的方法求最值 |

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】“微信运动”已成为当下热门的运动方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
步数 性别 | 0-2000 | 2001-5000 | 5001-8000 | 8001-10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
附: 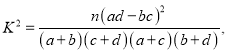
(1)已知某人一天的走路步数超过8000步被系统评定为“积极型”,否则为“懈怠型”,根据题意完成下面的 积极型 懈怠型 总计 男 女 总计 (2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.