题目内容
【题目】2019年12月,全国各中小学全体学生都参与了《禁毒知识》的答题竞赛,现从某校高一年级参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为![]() ,
,![]() ,…
,…![]() ).
).
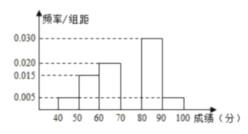
(1)求成绩在![]() 的频率,并补全此频率分布直方图;
的频率,并补全此频率分布直方图;
(2)求这次考试成绩的中位数的估计值;
(3)若从抽出的成绩在![]() 和
和![]() 的学生中任选两人,求他们的成绩在同一分组区间的概率.
的学生中任选两人,求他们的成绩在同一分组区间的概率.
【答案】(1)0.25;频率分布直方图见解析(2)74;(3)![]() .
.
【解析】
(1)根据频率之和等于![]() 公式即可求出成绩在
公式即可求出成绩在![]() 的频率.
的频率.
(2)先求前三组的频率之和为![]() ,前四组的频率之和为
,前四组的频率之和为![]() ,则中位数落在第四组,设中位数为
,则中位数落在第四组,设中位数为![]() ,根据公式
,根据公式![]() 即可求出中位数.
即可求出中位数.
(3)先算出成绩在![]() 和成绩在
和成绩在![]() 的人数,分别设为
的人数,分别设为![]() ,
,![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() ,再列举从中任选两人的结果和成绩在同一分组区间的结果,最后求概率即可.
,再列举从中任选两人的结果和成绩在同一分组区间的结果,最后求概率即可.
解:(1)第四小组的频率![]() .
.
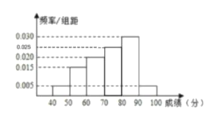
(2)第一组![]() 的频率
的频率![]() ,
,
第二组![]() 的频率
的频率![]() ,
,
第三组![]() 的频率
的频率![]() ,
,
第四组![]() 的频率
的频率![]()
前三组的频率之和为![]() ,前四组的频率之和为
,前四组的频率之和为![]() ,
,
所以中位数落在第四组,设中位数为![]() ,
,
则有:![]() ,∴
,∴![]() ,
,
所以这次考试成绩的中位数的估计值为74.
(3)由题意可知,成绩在![]() 的人数为
的人数为![]() ,
,
记他们分别为![]() ,
,![]() ,
,![]() ,成绩在
,成绩在![]() 的人数为
的人数为![]() ,
,
记他们分别为![]() ,
,![]() ,
,![]() ,
,
则从成绩在![]() 和
和![]() 的学生中任选两人的结果分别是:
的学生中任选两人的结果分别是:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共15种,
共15种,
事件他们的成绩在同一分组区间的结果是:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共6种,
,共6种,
所以所求事件的概率为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】C反应蛋白(CRP)是机体受到微生物入侵或组织损伤等炎症性刺激时细胞合成的急性相蛋白,医学认为CRP值介于0-10mg/L为正常值.下面是某患者在治疗期间连续5天的检验报告单中CRP值(单位:mg/L)与治疗大数的统计数据:
治疗天数x | 1 | 2 | 3 | 4 | 5 |
CRP值y | 51 | 40 | 35 | 28 | 21 |
(1)若CRP值y与治疗数x只有线性相关关系试用最小乘法求出y关于x的线性回归方程,并估计该者至少需要治疗多少天CRP值可以回到正常水平;
(2)为均衡城乡保障待遇,统一保障范同和支付准,为多保人员提供公平的基本医疗保障.某市城乡医疗保险实施办法指出:门诊报销比例为50%;住院报销比例,A类医疗机构80%,B类医疗机构60%.若张华参加了城乡基本医疗保险,他因CRP偏高选择在医疗机构治疗,医生为张华提供了三种治疗方案:方案一:门诊治疗,预计每天诊疗费80元;方案二:住院治疗,A类医疗机构,入院检查需花费600元,预计每天诊疗费100元;方案三:住院治疗,B类医疗机构,入院检查需花费400元,预计每天诊疗费40元;若张华需要经过连续治疗n天![]() ,请你为张华选择最经济实惠的治疗方案.
,请你为张华选择最经济实惠的治疗方案.
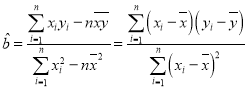 ,
,![]()