题目内容
【题目】如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N. 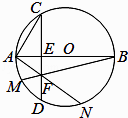
(1)求证:B、E、F、N四点共圆;
(2)求证:AC2+BFBM=AB2 .
【答案】
(1)证明:连结BN,
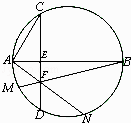
则AN⊥BN,
又CD⊥AB,
则∠BEF=∠BNF=90°,即∠BEF+∠BNF=180°,
则B、E、F、N四点共圆
(2)证明:由直角三角形的射影原理可知AC2=AEAB,
由Rt△BEF与Rt△BMA相似可知: ![]() ,
,
∴BFBM=BABE=BA(BA﹣EA),
∴BFBM=AB2﹣ABAE,
∴BFBM=AB2﹣AC2,即AC2+BFBM=AB2
【解析】(1)连结BN,证明∠BEF+∠BNF=180°,即可证明B、E、F、N四点共圆;(2)由直角三角形的射影原理可知AC2=AEAB,由Rt△BEF与Rt△BMA相似可知: ![]() ,即可得出结论.
,即可得出结论.

练习册系列答案
相关题目
【题目】某产品在某销售点的零售价x(单位:元)与每天的销售量y(单位:个)的统计数据如表所示:
x | 16 | 17 | 18 | 19 |
y | 50 | 34 | 41 | 31 |
由表可得回归直线方程 ![]() 中的
中的 ![]() ,根据模型预测零售价为20元时,每天的销售量约为( )
,根据模型预测零售价为20元时,每天的销售量约为( )
A.30
B.29
C.27.5
D.26.5