题目内容

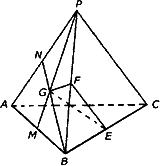
P是△ABC所在平面外一点，PA、PB、PC两两垂直，G为△PAB的重心，E、F分别是BC、PB上的点，且BE∶EC＝PF∶FB＝，求证：平面GEF⊥平面PBC

答案：
解析：

　　解析：∵G为△PAB的重心，∴　∴GF∥PA．

　　∵PA⊥PB　PA⊥PC，∴PA⊥面PBC．∴GF⊥面PBC，∴面GFE⊥面PBC．


练习册系列答案
相关题目
设P是△ABC所在平面上一点，且
CA
-
CP
=
CP
-
CB
，若△ABC的面积为2，则△PBC面积为（　　）
A、
1
2
B、1
C、2
D、4
设P是△ABC所在平面内的一点，
BC
+
BA
=2
BP
，则（　　）
在△ABC中，
AB
•
AC
=0．
（1）若P是△ABC所在平面上一点，且|
AP
|=2，∠CAP为锐角，
AP
•
AC
=2
AP
•
AB
=2，求|
AB
+
AC
+
AP
|的最小值．
（2）满足条件（1）的点P能否在△ABC的边BC上？并说明理由．
已知P是△ABC所在平面外一点，点O是点P在平面ABC上的射影．若PA=PB=PC，则O是△ABC的（　　）
设P是△ABC所在平面内一点，若(15sinA)
PA
+(12sinB)
PB
+(10sinC)
PC
=
0
且
BA
+
BC
=3
BP
则下列正确的命题序号是
①③④
①③④
．
①P是△ABC的重心    ②△ABC是锐角三角形  ③△ABC的三边长有可能是三个连续的整数  ④∠C=2∠A．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网