题目内容
在△ABC中，
•
=0．
（1）若P是△ABC所在平面上一点，且|
|=2，∠CAP为锐角，
•
=2
•
=2，求|
+
+
|的最小值．
（2）满足条件（1）的点P能否在△ABC的边BC上？并说明理由．
| AB |
| AC |
（1）若P是△ABC所在平面上一点，且|
| AP |
| AP |
| AC |
| AP |
| AB |
| AB |
| AC |
| AP |
（2）满足条件（1）的点P能否在△ABC的边BC上？并说明理由．
分析：（1）设∠CAP=α，可得∠BAP=
-α，结合
•
=2
•
=2且|
|=2，可得|
|=
，|
|=
．利用向量模的性质，可得|
+
+
|2的表达式，再利用基本不等式即可算出|
+
+
|的最小值．
（2）由（1）中|
|=
且|
|=
，可求出直线AB的方程含有参数α的形式，再将P点坐标代入直线方程加以验证，即可得到结论是否成立．
| π |
| 2 |
| AP |
| AC |
| AP |
| AB |
| AP |
| AC |
| 1 |
| cosα |
| AB |
| 1 |
| 2sinα |
| AB |
| AC |
| AP |
| AB |
| AC |
| AP |
（2）由（1）中|
| AC |
| 1 |
| cosα |
| AB |
| 1 |
| 2sinα |
解答：解：（1）∵△ABC中，
•
=0，∴
⊥
设∠CAP=α，α∈（0，
），则∠BAP=
-α，
又∵
•
=2
•
=2，|
|=2，
∴|
|•|
|cosα=2|
|•|
|cos（
-α）=2，可得|
|=
，|
|=
，
因此，|
+
+
|2=|
|2+|
|2+|
|2+2
•
+2
+2
•
=
+
+10=
+
+
≥
故|
+
+
|的最小值为
（2）满足条件（1）的点P不能在△ABC的边BC上，理由如下：
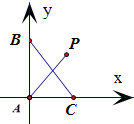
以C为坐标原点，分别以AC、AB为x、y轴正方向建立坐标系，
由（1）中|
|=
，|
|=
，
可得直线AB的方程的方程为xcosα+2ysinα=1
又∵|
|=2，∠CAP=α，
故P点坐标为（2cosα，2sinα），
将P代入AB的方程得2cos2α+4sin2α=2+2sin2α＞1，矛盾
故P点不在△ABC的边BC上
| AB |
| AC |
| AB |
| AC |
设∠CAP=α，α∈（0，
| π |
| 2 |
| π |
| 2 |
又∵
| AP |
| AC |
| AP |
| AB |
| AP |
∴|
| AP |
| AC |
| AP |
| AB |
| π |
| 2 |
| AC |
| 1 |
| cosα |
| AB |
| 1 |
| 2sinα |
因此，|
| AB |
| AC |
| AP |
| AB |
| AC |
| AP |
| AB |
| AC |
| AP |
| •AB |
| AC |
| AP |
=
| 1 |
| 4sin2α |
| 1 |
| cos2α |
| sin2α |
| cos2α |
| cos2α |
| 4sin2α |
| 45 |
| 4 |
| 49 |
| 4 |
故|
| AB |
| AC |
| AP |
| 7 |
| 2 |
（2）满足条件（1）的点P不能在△ABC的边BC上，理由如下：
以C为坐标原点，分别以AC、AB为x、y轴正方向建立坐标系，
由（1）中|
| AC |
| 1 |
| cosα |
| AB |
| 1 |
| 2sinα |
可得直线AB的方程的方程为xcosα+2ysinα=1
又∵|
| AP |
故P点坐标为（2cosα，2sinα），
将P代入AB的方程得2cos2α+4sin2α=2+2sin2α＞1，矛盾
故P点不在△ABC的边BC上
点评：本题给出向量关系式，求动点的轨迹方程并讨论模的最小值和点P位置等问题．着重考查了向量的模、基本不等式和点与直线的关系等知识点，属于难题．
练习册系列答案
相关题目