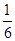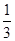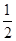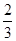题目内容
某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠.若该电梯在底层载有5位乘客,且每位乘客在这三层的每一层下电梯的概率均为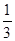 ,用ξ表示这5位乘客在第20层下电梯的人数.求:
,用ξ表示这5位乘客在第20层下电梯的人数.求:
(1)随机变量ξ的分布列;
(2)随机变量ξ的期望和方差.
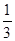 ,用ξ表示这5位乘客在第20层下电梯的人数.求:
,用ξ表示这5位乘客在第20层下电梯的人数.求:(1)随机变量ξ的分布列;
(2)随机变量ξ的期望和方差.
(1)
(2)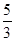
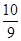
| ξ | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 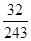 | 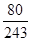 | 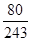 | 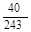 | 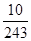 | 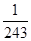 |
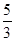
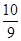
本试题主要是考查了分布列的求解和数学期望公式的运用。尤其是对于二项分布的正确理解和运用,是解决试题的关键。
解:(Ⅰ)考察一位乘客是否在第20层下电梯为一次试验,这是5次独立重复试验.
故ξ~B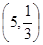 ,即有P(ξ=k)=C
,即有P(ξ=k)=C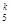
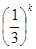
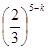 ,k=0,1,2,3,4,5. 4分
,k=0,1,2,3,4,5. 4分
从而ξ的分布列为
8分
(Ⅱ)由(Ⅰ)得Eξ=np=5×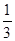 =
=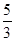 ;Dξ=npq=5×
;Dξ=npq=5×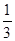 ×
×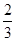 =
=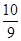 .
.
解:(Ⅰ)考察一位乘客是否在第20层下电梯为一次试验,这是5次独立重复试验.
故ξ~B
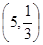 ,即有P(ξ=k)=C
,即有P(ξ=k)=C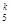
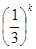
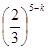 ,k=0,1,2,3,4,5. 4分
,k=0,1,2,3,4,5. 4分从而ξ的分布列为
| ξ | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 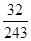 | 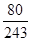 | 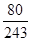 | 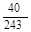 | 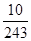 | 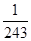 |
(Ⅱ)由(Ⅰ)得Eξ=np=5×
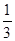 =
=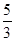 ;Dξ=npq=5×
;Dξ=npq=5×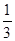 ×
×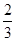 =
=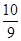 .
.
练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目



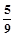
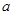 ,再由乙猜甲刚才想的数字,把乙猜的数字记为
,再由乙猜甲刚才想的数字,把乙猜的数字记为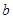 ,且
,且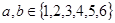 ,若
,若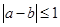 ,则称“甲乙心有灵犀”, 现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________.
,则称“甲乙心有灵犀”, 现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________.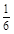 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。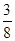

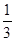
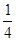
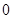 到
到 这十个数字中任选,某人忘记后一个号码,那么此人开锁时,在对好前两位数码后,随意拨动最后一个数字恰好能开锁的概率为____________
这十个数字中任选,某人忘记后一个号码,那么此人开锁时,在对好前两位数码后,随意拨动最后一个数字恰好能开锁的概率为____________ 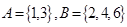 ,现从A, B中各取一个数字, 组成无重复数字的二位数, 在这些二位数
,现从A, B中各取一个数字, 组成无重复数字的二位数, 在这些二位数 中, 任取一个数, 则恰为奇数的概率为 ___ .
中, 任取一个数, 则恰为奇数的概率为 ___ . 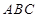 中,
中,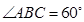 ,
,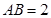 ,
,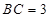 ,在
,在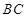 上任取一点
上任取一点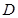 ,使△
,使△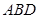 为钝角三角形的概率为
为钝角三角形的概率为