题目内容

如图所示，已知△ABC中DE∥FG∥BC，AD∶DF∶FB＝2∶3∶4．

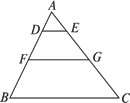
求：S△ADE∶S四边形DEGF∶S四边形BCGF．

答案：
解析：

　　解：因为AD∶DF＝2∶3，

　　所以AD∶AF＝2∶5．

　　所以S△ADE∶S△AFG＝4∶25．

　　因为AD∶DF∶FB＝2∶3∶4，

　　所以AD∶AB＝2∶9．

　　所以S△ADE∶S△ABC＝4∶81．

　　所以S△ADE∶S四边形DEGF∶S四边形BCGF＝4∶21∶56．

　　分析：在三角形中加了两条平行线出现了三个相似三角形，把大三角形分成了三部分，求三部分的面积比，分别求△ADE与△AFG的相似比，△ADE与△ABC的相似比，能得到△ADE与△AFG的面积比，△ADE与△ABC的面积比，问题可求．


练习册系列答案
相关题目
4、如图所示，已知AB⊥平面BCD，BC⊥CD，则图中互相垂直的平面有（　　）
如图所示，已知AB⊥平面BCD，M、N分别是AC、AD的中点，BC⊥CD．
（1）求证：MN∥平面BCD；
（2）求证：平面BCD⊥平面ABC；
（3）若AB=1，BC=
3
，求直线AC与平面BCD所成的角．
A：如图所示，已知AB为⊙O的直径，AC为弦，OD∥BC，交AC于点D，BC=4cm，
（1）试判断OD与AC的关系；
（2）求OD的长；
（3）若2sinA-1=0，求⊙O的直径．
B：（选修4-4）已知直线l经过点P（1，1），倾斜角α=
3π4
．
（1）写出直线l的参数方程；
（2）设l与圆x2+y2=4相交于两点A、B，求点P到A、B两点的距离之积．
一次机器人足球比赛中，甲队1号机器人由点A开始作匀速直线运动，到达点B时，发现足球在点D处正以2倍于自己的速度向点A作匀速直线滚动．如图所示，已知AB=4
2
dm，AD=17dm，∠BAC=45°．若忽略机器人原地旋转所需的时间，则该机器人最快可在何处截住足球？
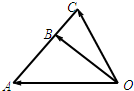精英家教网如图所示，已知
AB
=2
BC
，
OA
=
a
，
OB
=
b
，
OC
=
c
，则
c
=
 
．（用
a
，
b
表示）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网