题目内容
 如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.
如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.(1)求证:MN∥平面BCD;
(2)求证:平面BCD⊥平面ABC;
(3)若AB=1,BC=
| 3 |
分析:(1)因为M,N分别是AC,AD的中点,所以MN∥CD.由此能够证明MN∥平面BCD.
(2)因为AB⊥平面BCD,CD?平面BCD,所以AB⊥CD.因为CD⊥BC且AB∩BC=B,所以CD⊥平面ABC.由此能够证明平面BCD⊥平面ABC.
(3)因为AB⊥平面BCD,所以∠ACB为直线AC与平面BCD所成的角.由此能够求出直线AC与平面BCD所成的角.
(2)因为AB⊥平面BCD,CD?平面BCD,所以AB⊥CD.因为CD⊥BC且AB∩BC=B,所以CD⊥平面ABC.由此能够证明平面BCD⊥平面ABC.
(3)因为AB⊥平面BCD,所以∠ACB为直线AC与平面BCD所成的角.由此能够求出直线AC与平面BCD所成的角.
解答:解:(1)∵M,N分别是AC,AD的中点,
∴MN∥CD.
∵MN?平面BCD且CD?平面BCD,
∴MN∥平面BCD.
(2)∵AB⊥平面BCD,CD?平面BCD,
∴AB⊥CD.
∵CD⊥BC且AB∩BC=B,
∴CD⊥平面ABC.
∵CD?平面BCD,
∴平面BCD⊥平面ABC.
(3)∵AB⊥平面BCD,
∴∠ACB为直线AC与平面BCD所成的角.
在直角△ABC中,AB=1,BC=
,
∴tan∠ACB=
=
.
∴∠ACB=30°.
故直线AC与平面BCD所成的角为30°.
∴MN∥CD.
∵MN?平面BCD且CD?平面BCD,
∴MN∥平面BCD.
(2)∵AB⊥平面BCD,CD?平面BCD,
∴AB⊥CD.
∵CD⊥BC且AB∩BC=B,
∴CD⊥平面ABC.
∵CD?平面BCD,
∴平面BCD⊥平面ABC.
(3)∵AB⊥平面BCD,
∴∠ACB为直线AC与平面BCD所成的角.
在直角△ABC中,AB=1,BC=
| 3 |
∴tan∠ACB=
| AB |
| BC |
| ||
| 3 |
∴∠ACB=30°.
故直线AC与平面BCD所成的角为30°.
点评:本题考查直线与平面平行、平面与平面垂直的证明,考查直线与平面所成角的求法.解题时要认真审题,仔细解答,注意合理地化立体问题为平面问题.

练习册系列答案
相关题目

 A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm,
A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm, 一次机器人足球比赛中,甲队1号机器人由点A开始作匀速直线运动,到达点B时,发现足球在点D处正以2倍于自己的速度向点A作匀速直线滚动.如图所示,已知
一次机器人足球比赛中,甲队1号机器人由点A开始作匀速直线运动,到达点B时,发现足球在点D处正以2倍于自己的速度向点A作匀速直线滚动.如图所示,已知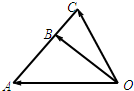 如图所示,已知
如图所示,已知