题目内容
 A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm,
A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm,(1)试判断OD与AC的关系;
(2)求OD的长;
(3)若2sinA-1=0,求⊙O的直径.
B:(选修4-4)已知直线l经过点P(1,1),倾斜角α=
| 3π | 4 |
(1)写出直线l的参数方程;
(2)设l与圆x2+y2=4相交于两点A、B,求点P到A、B两点的距离之积.
分析:A:(1)根据直径所对的圆周角为直角,以及三角形的中位线定理,可得AC⊥OD;
(2)在△ACB中,BC=4cm且OD是中位线,根据三角形的中位线定理,得OD=
BC=2cm;
(3)Rt△ADO中,利用正弦的定义结合OD=2cm,得到半径OA=4cm,从而得到⊙O的直径长.
B:(1)根据直线的参数方程关于倾斜角的公式,得参数方程为
(t为参数),再化简整理即可;
(2)将点(1-
t,1+
t)代入圆x2+y2=4的方程中,再化简整理得:t2=2,设方程的两个根为 t1,t2,根据参数方程中t的几何意义结合一元二次方程根与系数的关系,得到点P到A、B两点的距离之积|t1||t2|=|t1t2|=2.
(2)在△ACB中,BC=4cm且OD是中位线,根据三角形的中位线定理,得OD=
| 1 |
| 2 |
(3)Rt△ADO中,利用正弦的定义结合OD=2cm,得到半径OA=4cm,从而得到⊙O的直径长.
B:(1)根据直线的参数方程关于倾斜角的公式,得参数方程为
|
(2)将点(1-
| ||
| 2 |
| ||
| 2 |
解答:解:(A)(1)∵AB为⊙O的直径,
∴∠C=90°,即AC⊥BC,又∵OD∥BC,
∴AC⊥OD…(3分)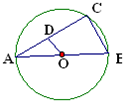
(2)∵O为AB中点,OD∥BC
∴OD为△ACB的中位线
∴OD=
BC=2cm…(6分)
(3)∵2sinA-1=0,∴sinA=
∴Rt△ADO中,sinA=
=
,
又∵OD=2cm,
∴OA=4cm,
因为半径等于4cm,所以⊙O的直径是8cm…(10分)
(B)(1)由题意,可得直线的参数方程为
(t为参数)
整理得
(t为参数)…(3分)
(2)把
代入圆x2+y2=4的方程中,得(1-
t)2+(1+
t)2=4
整理得:t2=2,设方程的两个根为 t1,t2,则
…(7分)
由参数方程中t的几何意义可知|t1|,|t2|即为点P到A、B两点的距离,
∴点P到A、B两点的距离之积|t1||t2|=|t1t2|=2…(10分)
∴∠C=90°,即AC⊥BC,又∵OD∥BC,
∴AC⊥OD…(3分)

(2)∵O为AB中点,OD∥BC
∴OD为△ACB的中位线
∴OD=
| 1 |
| 2 |
(3)∵2sinA-1=0,∴sinA=
| 1 |
| 2 |
∴Rt△ADO中,sinA=
| OD |
| OA |
| 1 |
| 2 |
又∵OD=2cm,
∴OA=4cm,
因为半径等于4cm,所以⊙O的直径是8cm…(10分)
(B)(1)由题意,可得直线的参数方程为
|
整理得
|
(2)把
|
| ||
| 2 |
| ||
| 2 |
整理得:t2=2,设方程的两个根为 t1,t2,则
|
由参数方程中t的几何意义可知|t1|,|t2|即为点P到A、B两点的距离,
∴点P到A、B两点的距离之积|t1||t2|=|t1t2|=2…(10分)
点评:本题第一问给出一个平面几何证明问题,着重考查了圆有关的比例线段和三角函数在直角三角形中的定义;第二问结合直线方程的参数方程形式,着重考查了直线的基本量与基本形式和参数方程中参数的意义等知识点,都属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
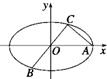 如图所示,已知A、B、C是椭圆E:
如图所示,已知A、B、C是椭圆E: 如图所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
如图所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P. 水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为
水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为 如图所示,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是
如图所示,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是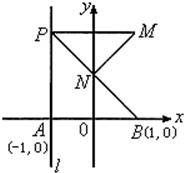 (2007•崇文区二模)如图所示,已知A(-1,0),B(1,0),直线l垂直AB于A点,P为l上一动点,点N为线段BP上一点,且满足
(2007•崇文区二模)如图所示,已知A(-1,0),B(1,0),直线l垂直AB于A点,P为l上一动点,点N为线段BP上一点,且满足