题目内容
 一次机器人足球比赛中,甲队1号机器人由点A开始作匀速直线运动,到达点B时,发现足球在点D处正以2倍于自己的速度向点A作匀速直线滚动.如图所示,已知AB=4
一次机器人足球比赛中,甲队1号机器人由点A开始作匀速直线运动,到达点B时,发现足球在点D处正以2倍于自己的速度向点A作匀速直线滚动.如图所示,已知AB=4| 2 |
分析:构建三角形ABC,利用余弦定理,建立方程,即可求得机器人最快可在何处截住足球.
解答:解:设该机器人最快可在点C处截住足球,点C在线段AD上,设BC=xdm. (2分)
由题意,CD=2xdm.AC=AD-CD=(17-2x)(dm). (4分)
在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB•ACcosA. (6分)
即x2=(4
)2+(17-2x)2-2×4
×(17-2x)cos45°. (8分)
解得x1=5(dm),x2=
(dm). (10分)
∴AC=17-2x=7(dm),或AC=-
(dm)(不合题意,舍去). (11分)
答:该机器人最快可在线段AD上离点A7dm的点C处截住足球. (12分)
由题意,CD=2xdm.AC=AD-CD=(17-2x)(dm). (4分)
在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB•ACcosA. (6分)
即x2=(4
| 2 |
| 2 |
解得x1=5(dm),x2=
| 37 |
| 3 |
∴AC=17-2x=7(dm),或AC=-
| 23 |
| 3 |
答:该机器人最快可在线段AD上离点A7dm的点C处截住足球. (12分)
点评:本题考查余弦定理的运用,考查利用数学知识解决实际问题,解题的关键是构建满足题意的三角形,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目

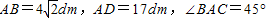 .若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球?
.若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球?