题目内容
 如图所示,在矩形ABCD中,已知AB=a,BC=b.a≤3b,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且都等于x,则四边形EFGH面积的最大值为
如图所示,在矩形ABCD中,已知AB=a,BC=b.a≤3b,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且都等于x,则四边形EFGH面积的最大值为分析:题意可得a>b>0,a≤3b,四边形EFGH面积S=ab-2[
x2+
(a-x)(b-x)]=-2x2+(a+b)x,0<x≤b.再利用二次函数的性质求得它的最大值.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由题意可得a>b>0,a≤3b,且S△AEH=S△CFG=
x2,S△BEF=S△DGH=
(a-x)(b-x),且 0<x≤b.
故四边形EFGH面积S=ab-2[
x2+
(a-x)(b-x)]=-2x2+(a+b)x.
再由a≤3b可得
≤b,故当x=
时,S取得最大值为
,
故答案为
.
| 1 |
| 2 |
| 1 |
| 2 |
故四边形EFGH面积S=ab-2[
| 1 |
| 2 |
| 1 |
| 2 |
再由a≤3b可得
| a+b |
| 4 |
| a+b |
| 4 |
| (a+b)2 |
| 8 |
故答案为
| (a+b)2 |
| 8 |
点评:本题主要考查二次函数的性质应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
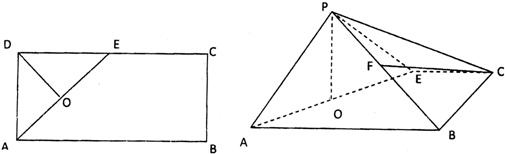 19、如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且PC=PB,F是BP的中点.
19、如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且PC=PB,F是BP的中点.
 如图所示,在矩形ABCD中,AB=4cm,BC=2cm,在图形上随机撒一粒黄豆,则黄豆落到圆上的概率是
如图所示,在矩形ABCD中,AB=4cm,BC=2cm,在图形上随机撒一粒黄豆,则黄豆落到圆上的概率是