题目内容
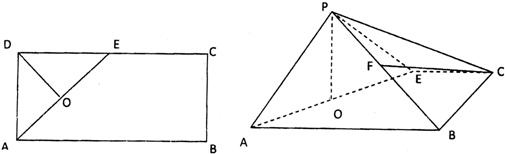 19、如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且PC=PB,F是BP的中点.
19、如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且PC=PB,F是BP的中点.(Ⅰ)求证:CF∥面APE;
(Ⅱ)求证:PO⊥面ABCE.
分析:(Ⅰ)欲证CF∥面APE,而FC?平面FGC,可先证平面APE∥平面FGC,取AB中点G,连接GF,GC,易证四边形AECG为平行四边形,则AE∥GC,而GF∥AP,GF∩GC=G,AE∩AP=A,满足面面平行的判定定理所需条件;
(Ⅱ)欲证PO⊥面ABCE,根据直线与平面垂直的判定定理可知只需证PO与面ABCE内两相交直线垂直,取BC的中点H,连OH,PH,根据线面垂直的判定定理可知BC⊥面POH,则BC⊥PO,而PO⊥AE,又BC与AE相交满足定理条件.
(Ⅱ)欲证PO⊥面ABCE,根据直线与平面垂直的判定定理可知只需证PO与面ABCE内两相交直线垂直,取BC的中点H,连OH,PH,根据线面垂直的判定定理可知BC⊥面POH,则BC⊥PO,而PO⊥AE,又BC与AE相交满足定理条件.
解答: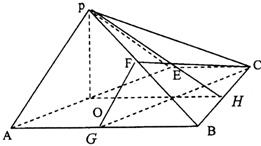 解:(Ⅰ)取AB中点G,连接GF,GC,∵EC∥AB,EC=AB,∴四边形AECG为平行四边形,∴AE∥GC,(2分)
解:(Ⅰ)取AB中点G,连接GF,GC,∵EC∥AB,EC=AB,∴四边形AECG为平行四边形,∴AE∥GC,(2分)
在△ABP中,GF∥AP(3分)
又GF∩GC=G,AE∩AP=A
所以平面APE∥平面FGC(5分)
又FC?平面FGC
所以,CF∥面APE(6分)
(Ⅱ)PA=PE,OA=OE∴PO⊥AE
取BC的中点H,连OH,PH,∴OH∥AB,∴OH⊥BC
因为PB=PC∴BC⊥PH,所以BC⊥面POH
从而BC⊥PO(10分)
又BC与AE相交,可得PO⊥面ABCE(12分)
 解:(Ⅰ)取AB中点G,连接GF,GC,∵EC∥AB,EC=AB,∴四边形AECG为平行四边形,∴AE∥GC,(2分)
解:(Ⅰ)取AB中点G,连接GF,GC,∵EC∥AB,EC=AB,∴四边形AECG为平行四边形,∴AE∥GC,(2分)在△ABP中,GF∥AP(3分)
又GF∩GC=G,AE∩AP=A
所以平面APE∥平面FGC(5分)
又FC?平面FGC
所以,CF∥面APE(6分)
(Ⅱ)PA=PE,OA=OE∴PO⊥AE
取BC的中点H,连OH,PH,∴OH∥AB,∴OH⊥BC
因为PB=PC∴BC⊥PH,所以BC⊥面POH
从而BC⊥PO(10分)
又BC与AE相交,可得PO⊥面ABCE(12分)
点评:本题主要考查了线面平行的判定,以及线面垂直的判定,同时考查了空间想象能力、推理论证的能力.

练习册系列答案
相关题目

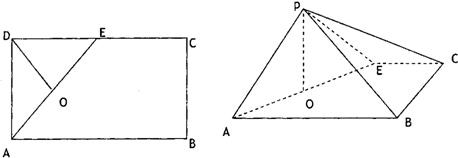
 如图所示,在矩形ABCD中,AB=4cm,BC=2cm,在图形上随机撒一粒黄豆,则黄豆落到圆上的概率是
如图所示,在矩形ABCD中,AB=4cm,BC=2cm,在图形上随机撒一粒黄豆,则黄豆落到圆上的概率是 如图所示,在矩形ABCD中,已知AB=a,BC=b.a≤3b,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且都等于x,则四边形EFGH面积的最大值为
如图所示,在矩形ABCD中,已知AB=a,BC=b.a≤3b,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且都等于x,则四边形EFGH面积的最大值为