题目内容
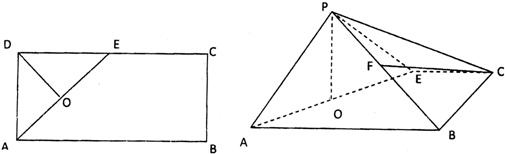
19、如图所示，在矩形ABCD中，AB=4，AD=2，E是CD的中点，O为AE的中点，F是AB的中点．以AE为折痕将△ADE向上折起，使面DAE⊥面ABCE．
（1）求证：OF∥面BDE；
（2）求证：AD⊥面BDE．
（1）求证：OF∥面BDE；
（2）求证：AD⊥面BDE．
分析：（1）根据O为AE的中点，F是AB的中点则OF∥BE，BE⊆面BDE，OF不属于面BDE，根据直线与平面平行的判定定理可知OF∥面BDE；
（2）根据面DAE⊥面ABCE，BE⊥AE，则BE⊥面ADE，而AD⊆面ADE，则BE⊥AD，AD⊥DE，且DE∩BE=E，满足直线与平面垂直的判定定理，则AD⊥面BDE．
（2）根据面DAE⊥面ABCE，BE⊥AE，则BE⊥面ADE，而AD⊆面ADE，则BE⊥AD，AD⊥DE，且DE∩BE=E，满足直线与平面垂直的判定定理，则AD⊥面BDE．
解答：
证明：（1）O为AE的中点，F是AB的中点，OF∥BE
BE⊆面BDE，OF不属于面BDE，
∴OF∥面BDE
（2）面DAE⊥面ABCE，BE⊥AE
∴BE⊥面ADE，AD⊆面ADE
∴BE⊥ADAD⊥DE，且DE∩BE=E，
∴AD⊥面BDE
证明：（1）O为AE的中点，F是AB的中点，OF∥BEBE⊆面BDE，OF不属于面BDE，
∴OF∥面BDE
（2）面DAE⊥面ABCE，BE⊥AE
∴BE⊥面ADE，AD⊆面ADE
∴BE⊥ADAD⊥DE，且DE∩BE=E，
∴AD⊥面BDE
点评：本题主要考查了直线与平面平行的判定，以及直线与平面垂直的判定，线面平行常常找线线平行或面面平行进行证明，属于中档题．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
19、如图所示，在矩形ABCD中，AB=4，AD=2，E是CD的中点，O为AE的中点，以AE为折痕将△ADE向上折起，使D到P点位置，且PC=PB，F是BP的中点．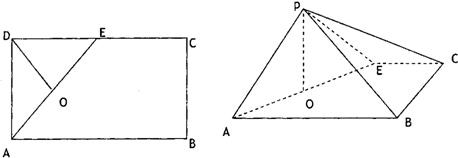
如图所示，在矩形ABCD中，AB=4cm，BC=2cm，在图形上随机撒一粒黄豆，则黄豆落到圆上的概率是
如图所示，在矩形ABCD中，已知AB=a，BC=b．a≤3b，在AB，AD，CD，CB上分别截取AE，AH，CG，CF，且都等于x，则四边形EFGH面积的最大值为