题目内容
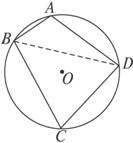
已知圆内接四边形ABCD的边长分别为AB=2,BC=6,CD=DA=4,求四边形ABCD的面积.
解:如图,连结BD,则有四边形ABCD的面积S=S△ABD+S△CDB=
AB·ADsinA+
BC·CDsinC.
∵A+C=180°,∴sinA=sinC.
故S=
(AB·AD+BC·CD)·sinA=
(2×4+6×4)sinA=16sinA.
由余弦定理,在△ABD中,BD2=AB2+AD2-2AB·ADcosA=20-16cosA;
在△CDB中,BD2=CB2+CD2-2CB·CDcosC=52-48cosC.
∴20-16cosA=52-48cosC.
∵cosC=-cosA,
∴64cosA=-32,cosA=-
.
又0°＜A＜180°,
∴A=120°.故S=16sin120°=8
.
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
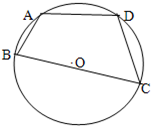如图，已知圆内接四边形ABCD的边长分别为AB=2，BC=6，AD=CD=4．
如图，已知圆内接四边形ABCD的边长为AB=2，BC=6，CD=DA=4，则四边形ABCD面积为（ ）
如图已知圆内接四边形ABCD中，AB=2，BC=6，AD=CD=4，则四边形ABCD的面积S=