题目内容
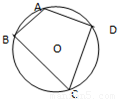
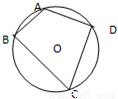
如图已知圆内接四边形ABCD中，AB=2，BC=6，AD=CD=4，则四边形ABCD的面积S=8
| 3 |
8
．| 3 |
分析：利用余弦定理求出A，C的关系，结合圆内接四边形的对角和为180°，求出A的值，利用三角形的面积的和，求出四边形的面积即可．
解答：解：由余弦定理得BD2=4+16-2×2×4cosA=20-16cosA，
又BD2=16+36-2×4×6cosC=52-48cosC，
∵A+C=180°，
∴20-16cosA=52+48cosA，解得cosA=-
，
∴A=120°．
SABCD=S△ABD+S△CBD=
×2×4×sin120°+
×4×6×sin60°=8
．
故答案为：8
又BD2=16+36-2×4×6cosC=52-48cosC，
∵A+C=180°，
∴20-16cosA=52+48cosA，解得cosA=-
| 1 |
| 2 |
∴A=120°．
SABCD=S△ABD+S△CBD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
故答案为：8
| 3 |
点评：本题主要考查了余弦定理，以及三角形的面积公式的应用，同时考查了运算求解的能力，属于基础题．
练习册系列答案
相关题目
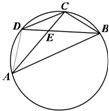如图，在圆内接四边形ABCD中，对角线AC，BD相交于点E．已知
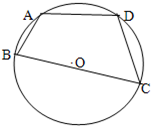如图，已知圆内接四边形ABCD的边长分别为AB=2，BC=6，AD=CD=4．
