题目内容
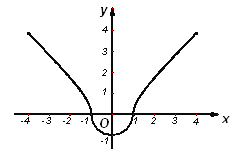
【题目】已知曲线![]() .
.
(1)用函数![]() 的形式表示曲线
的形式表示曲线![]() ;
;
(2)若直线![]() 与曲线
与曲线![]() 有两个公共点,求实数
有两个公共点,求实数![]() 的取值范围;
的取值范围;
(3)若点![]() 的坐标为
的坐标为![]() ,
,![]() 为曲线
为曲线![]() 上的点,求
上的点,求![]() 的最小值.
的最小值.
【答案】(1)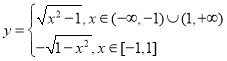 ; (2)
; (2)![]() ; (3)
; (3)![]() .
.
【解析】
(1)由曲线![]() ,当
,当![]() 时,得到
时,得到![]() ,当
,当![]() 时,得
时,得![]() ,即可求解;
,即可求解;
(2)根据直线与圆的位置关系,以及直线与双曲线的位置关系,结合图象,即可求解;
(3)分别求得当![]() 和
和![]() 时,
时,![]() 的最小值,即可求解.
的最小值,即可求解.
(1)由题意,曲线![]() ,
,
当![]() 时,曲线
时,曲线![]() ,则
,则![]() ,其中
,其中![]() ;
;
当![]() 时,曲线
时,曲线![]() ,则
,则![]() ,其中
,其中![]() ,
,
所以函数![]() 的解析式为
的解析式为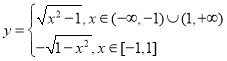 .
.
(2)若直线![]() 与曲线
与曲线![]() 有两个公共点,
有两个公共点,
则圆心到直线的距离满足![]() ,解得
,解得![]() ,
,
若直线![]() 与曲线
与曲线![]() 和
和![]() 各有一个公共点,
各有一个公共点,
其中曲线![]() 的渐近线的方程为
的渐近线的方程为![]() ,
,
则由图象可得![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.
(3)当![]() 时,
时,![]() ,
,
由![]() 得,当
得,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
又由![]() ,所以
,所以![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目