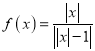题目内容
【题目】已知函数![]() .
.
(1)判断函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(2)函数![]() 在区间
在区间![]() 上的极值点从小到大分别为
上的极值点从小到大分别为![]() ,证明:
,证明:
(Ⅰ)![]() ;
;
(Ⅱ)对一切![]() 成立.
成立.
【答案】(1)两个零点;(2)(I)见解析;(Ⅱ)见解析
【解析】
(1)对![]() 求导,利用导数得出函数
求导,利用导数得出函数![]() 的单调性,结合零点存在性定理即可得出零点的个数;
的单调性,结合零点存在性定理即可得出零点的个数;
(2) (Ⅰ)对函数![]() 求导,由(1)得出
求导,由(1)得出![]() 的范围,进而得到
的范围,进而得到![]() ,利用诱导公式即可得出
,利用诱导公式即可得出![]() ;
;
(Ⅱ)由(Ⅰ)得出![]() >
>![]() >
>![]() ,结合
,结合![]() 的单调性确定
的单调性确定![]() ,且
,且![]() ,对n为偶数和奇数进行分类讨论,即可得出对一切
,对n为偶数和奇数进行分类讨论,即可得出对一切![]() 成立.
成立.
(1)![]()
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,![]() 在
在![]() 上无零点
上无零点
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]()
![]() 在
在![]() 上有唯一零点
上有唯一零点
当![]() 时,
时,![]() ,
,![]() 上单调递减
上单调递减
![]() ,
,![]() 上有唯一零点
上有唯一零点
综上,函数![]() 在区间
在区间![]() 上有两个零点。
上有两个零点。
(2)![]()
(I)由(1)知![]() 在
在![]() 无极值点;在
无极值点;在![]() 有极小值点,即为
有极小值点,即为![]() ;
;
在![]() 有极大值点,即为
有极大值点,即为![]() ,同理可得,在
,同理可得,在![]() 有极小值点
有极小值点![]() ,
,
在![]() 有极值点
有极值点![]() .由
.由![]() 得
得![]()
![]()
![]()
![]() ,
,![]() ,由函数
,由函数![]() 在
在![]() 单调递增,
单调递增,
得![]() ,
,![]() ,
,
由![]() 在
在![]() 单调递减得
单调递减得![]()
![]()
![]() ;
;
(Ⅱ)同理![]() ,
,![]() >
>![]() >
>![]()
由![]() 在
在![]() 上单调递减得
上单调递减得![]()
![]() ,且
,且![]()
当n为偶数时,从![]() 开始相邻两项配对,每组和均为负值,
开始相邻两项配对,每组和均为负值,
即![]() ,结论成立;
,结论成立;
当n为奇数时,从![]() 开始相邻两项配对,每组和均为负值,还多出最后一项也是负值,即
开始相邻两项配对,每组和均为负值,还多出最后一项也是负值,即![]() ,结论也成立。
,结论也成立。
综上,对一切![]() ,
,![]() 成立.
成立.

练习册系列答案
相关题目