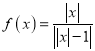题目内容
【题目】若函数![]() 与
与![]() 在给定的区间上满足
在给定的区间上满足![]() 恒成立,则称这两个函数在该区间上“和谐”。
恒成立,则称这两个函数在该区间上“和谐”。
(1)若函数![]() 与
与![]() 在R上和谐,求实数a的取值范围;
在R上和谐,求实数a的取值范围;
(2)若函数![]() 与
与![]() 在
在![]() 上和谐,求实数a的取值范围.
上和谐,求实数a的取值范围.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)由已知条件得,需![]() 都在
都在![]() 上恒成立,或
上恒成立,或![]() 有相同的两个不等的实根,即
有相同的两个不等的实根,即 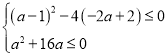 ,或
,或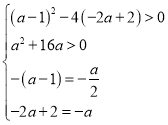 ,
,
可求得实数a的取值范围;
(2)由对数的定义域得![]() ,再由题意得
,再由题意得![]() ,由
,由![]() 和
和![]() ,可得
,可得![]() 和
和![]() ,再由
,再由![]() 讨论当
讨论当![]() 时,当
时,当![]() 时,当
时,当![]() 时,分别根据不等式的性质可得实数a的取值范围.
时,分别根据不等式的性质可得实数a的取值范围.
(1)由已知条件得,若函数![]() 与
与![]() 在R上和谐,
在R上和谐,
则需![]() 都在
都在![]() 上恒成立,或
上恒成立,或![]() 有相同的两个不等的实根,
有相同的两个不等的实根,
当![]() 都在
都在![]() 上恒成立时,则需
上恒成立时,则需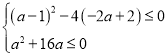 ,解得
,解得![]() ,所以
,所以![]() ;
;
当![]() 有相同的两个不等的实根时,
有相同的两个不等的实根时,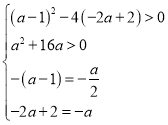 ,解得
,解得![]() ,
,
综上可得实数a的取值范围是![]() ;
;
(2)由对数的定义域可得![]() ,再由题意得
,再由题意得![]() ,
,
由![]() ,可得
,可得![]() ,所以
,所以![]() 时,
时,![]() ,
,![]() 时,
时,![]() ;
;
由![]() ,可得
,可得![]() ,所以
,所以![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
由题意要使函数![]() 与
与![]() 在
在![]() 上和谐,则
上和谐,则![]() 的两零点
的两零点![]() 之间必需无正整数,
之间必需无正整数,
又由于![]() ,所以
,所以
当![]() 时,
时,![]() ,
, ![]() ,
,![]() 之间有正整数,不满足题意;
之间有正整数,不满足题意;
当![]() 时,
时,![]() ,
, ![]() ,
,![]() 之间有正整数,不满足题意;
之间有正整数,不满足题意;
当![]() 时,
时,![]() ,满足题意.
,满足题意.
所以实数a的取值范围是![]() .
.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目