��Ŀ����
����Ŀ����ijѧУ�����꼶��800�������������ȡ50�˲������ߣ����ݱ���������ѧ������ȫ������155cm��195cm֮�䣬��������������·�ʽ�ֳɰ��飺��һ��[155��160�����ڶ���[160��165���������ڰ���[190��195]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪��һ����ڰ���������ͬ��������ȵ�������1�ˣ� 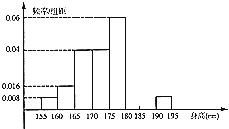
��1����������ѧУ�����꼶ȫ������������180cm���ϣ���180cm����������
��2�������������ڵ�����͵ڰ�������������������ȡ���ˣ������ǵ����߷ֱ�Ϊx��y�������㡰|x��y|��5�����¼��ĸ��ʣ�
���𰸡�
��1���⣺��Ƶ�ʷֲ�ֱ��ͼ��������180cm���ϣ���180cm��Ϊ������飬
���������Ƶ��Ϊ��0.016+0.012+0.008����5=0.18��
����ѧУ�����꼶ȫ������������180cm���ϣ���180cm��������Ϊ800��0.18=144
��2���⣺����֪��������[180��185���ڵ�����Ϊ4����Ϊa��b��c��d��
������[190��195]�ڵ�����Ϊ2����ΪA��B��
��x��y��[180��185��ʱ����ab��ac��ad��bc��bd��cd��6�������
��x��y��[190��195]ʱ����AB��1�������
��x��y�ֱ���[180��185����[190��195]��ʱ����aA��bA��cA��dA��aB��bB��cB��dB����8�������
���ԣ������¼�����Ϊ6+1+8=15��
�¼���|x��y|��5����ȡ��������ͬһ�飬���������Ļ����¼�������6+1=7��
����P��|x��y|��5��= ![]()
����������1����Ƶ�ʷֲ�ֱ��ͼ��������180cm���ϣ���180cm��Ϊ������飬����ɵ���������Ƶ�ʣ�����ȫУ������������������ɵø����꼶ȫ������������180cm������������2���������⣬�����ɵ�������[180��185���ڵ�����Ϊ4����Ϊa��b��c��d��������[190��195]�ڵ�����Ϊ2����ΪA��B�������оٴ�6����ȡ��2�˵�����������ɵû����¼��������¼���|x��y|��5���������Ļ����¼���Ŀ���ɹŵ����ʽ������ɵô�

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�