题目内容
19. 如图,在平面直角坐标系中,O为原点,点P(1,1)关于原点的对称点为R,点Q(3,2)关于x轴的对称点为K.
如图,在平面直角坐标系中,O为原点,点P(1,1)关于原点的对称点为R,点Q(3,2)关于x轴的对称点为K.(1)求作向量$\overrightarrow{OR}$、$\overrightarrow{RK}$;
(2)求作:$\overrightarrow{OP}$-$\overrightarrow{OQ}$;
(3)求作:$\overrightarrow{OQ}-\overrightarrow{OK}$.
分析 利用对称性可得R,K,再利用向量的运算及其作法即可得出.
解答 解:点P(1,1)关于原点的对称点为R(-1,-1),点Q(3,2)关于x轴的对称点为K(3,-2).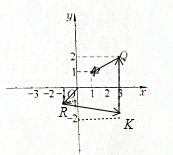
(1)如图所示,$\overrightarrow{OR}$=(-1,-1),$\overrightarrow{RK}$=(4,-1).
(2)$\overrightarrow{OP}-\overrightarrow{OQ}$=$\overrightarrow{QP}$,
(3)$\overrightarrow{OQ}-\overrightarrow{OK}$=$\overrightarrow{KQ}$.
点评 本题考查了对称性、向量的运算及其作法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.若如框图所给的程序运行结果为S=1,那么判断框中应填入的关于k的条件可以是( )


| A. | k=7 | B. | k≤6 | C. | k<6 | D. | k>6 |
8.一个组合体的主视图和左视图相同,如图,其体积为22π,则图中的x为( )


| A. | 4 | B. | 4.5 | C. | 5 | D. | 5.5 |
9.若0<x<y<1,则下列不等式正确的是( )
| A. | 4y<4x | B. | x3>y3 | C. | log4x<log4y | D. | ${(\frac{1}{4})^x}<{(\frac{1}{4})^y}$ |
