题目内容
数列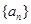 首项
首项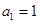 ,前
,前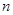 项和
项和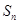 满足等式
满足等式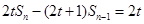 (常数
(常数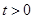 ,
,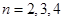 ……)
……)
(1)求证: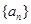 为等比数列;
为等比数列;
(2)设数列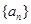 的公比为
的公比为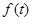 ,作数列
,作数列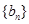 使
使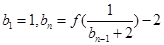 (
(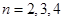 ……),求数列
……),求数列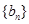 的通项公式.
的通项公式.
(3)设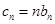 ,求数列
,求数列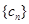 的前
的前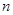 项和
项和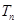 .
.
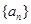 首项
首项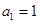 ,前
,前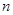 项和
项和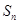 满足等式
满足等式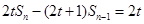 (常数
(常数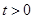 ,
,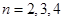 ……)
……)(1)求证:
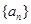 为等比数列;
为等比数列;(2)设数列
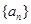 的公比为
的公比为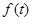 ,作数列
,作数列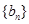 使
使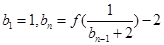 (
(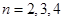 ……),求数列
……),求数列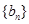 的通项公式.
的通项公式.(3)设
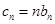 ,求数列
,求数列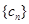 的前
的前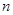 项和
项和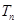 .
.(1)见解析 (2)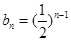 (3)
(3)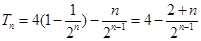
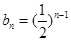 (3)
(3)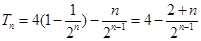
第一问利用由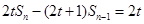 得
得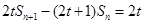
两式相减得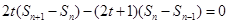
故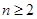 时,
时,
从而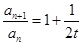 又
又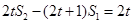 即
即 ,而
,而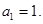
从而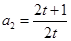 故
故
第二问中,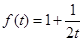
 又
又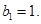 故
故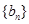 为等比数列,通项公式为
为等比数列,通项公式为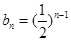
第三问中,
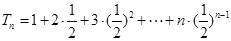 两边同乘以
两边同乘以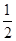
利用错位相减法得到和。
(1)由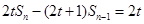 得
得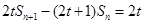
两式相减得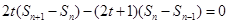
故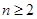 时,
时,
从而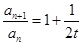 ………………3分
………………3分
又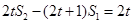 即
即 ,而
,而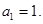
从而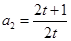 故
故
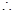 对任意
对任意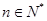 ,
,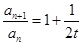 为常数,即
为常数,即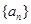 为等比数列………………5分
为等比数列………………5分
(2)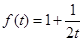
 ……………………7分
……………………7分
又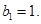 故
故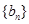 为等比数列,通项公式为
为等比数列,通项公式为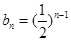 ………………9分
………………9分
(3)
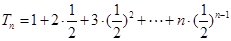 两边同乘以
两边同乘以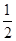
 ………………11分
………………11分
两式相减得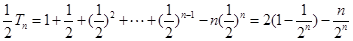
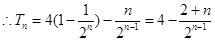
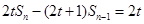 得
得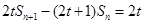
两式相减得
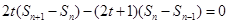
故
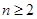 时,
时,
从而
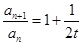 又
又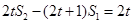 即
即 ,而
,而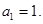
从而
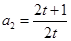 故
故
第二问中,
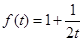
 又
又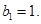 故
故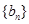 为等比数列,通项公式为
为等比数列,通项公式为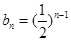
第三问中,

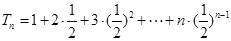 两边同乘以
两边同乘以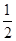
利用错位相减法得到和。
(1)由
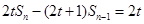 得
得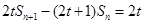
两式相减得
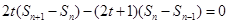
故
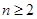 时,
时,
从而
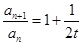 ………………3分
………………3分又
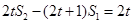 即
即 ,而
,而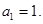
从而
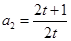 故
故
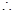 对任意
对任意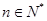 ,
,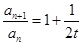 为常数,即
为常数,即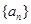 为等比数列………………5分
为等比数列………………5分(2)
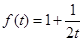
 ……………………7分
……………………7分又
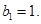 故
故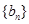 为等比数列,通项公式为
为等比数列,通项公式为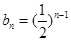 ………………9分
………………9分(3)

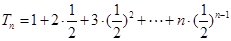 两边同乘以
两边同乘以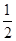
 ………………11分
………………11分两式相减得
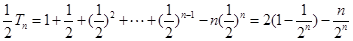
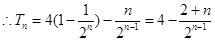

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
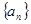 中,
中,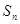 是前
是前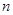 项和,且
项和,且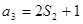 ,
,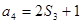 ,则
,则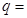 .
.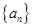 为等比数列,
为等比数列,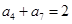 ,
,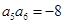 ,则
,则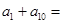 ( )
( )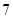
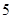
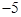
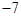
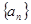 的前n项和为Sn,若
的前n项和为Sn,若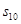 =2,
=2,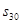 =14,则
=14,则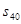 等于 ( )
等于 ( )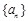 中,
中,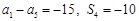 ,则
,则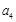 等于( )
等于( )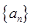 的前
的前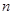 项和为
项和为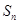 ,已知
,已知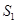 ,
,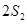 ,
,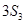 成等差数列,则
成等差数列,则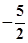
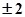
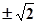
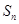 为等比数列
为等比数列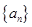 的前
的前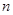 项和,已知
项和,已知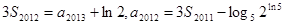 ,则公比
,则公比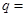 ( )
( )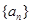 中,
中,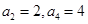 ,则
,则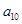 = ;
= ;