题目内容
已知命题p:对m∈[-1,1],不等式a2-5a+5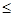
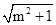 恒成立;命题q:方程x2+ax+2=0在实数集内没有解;若p和q都是真命题,求a的取值范围.
恒成立;命题q:方程x2+ax+2=0在实数集内没有解;若p和q都是真命题,求a的取值范围.

解析试题分析:∵m∈[-1,1],∴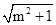 ∈[1,
∈[1,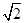 ].
].
∵对m∈[-1,1],不等式a2-5a+5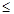
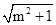 恒成立,可得a2-5a+5
恒成立,可得a2-5a+5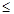 1,解得,
1,解得,
即p真:  ; 6分
; 6分
命题q:方程x2+ax+2=0在实数集内没有解;∴△=a2-8<0,
∴-2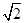 <a<2
<a<2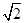 ,
,
即q真: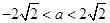 10分
10分
综上: 14分
14分
考点:命题,一元二次不等式解法,不等式恒成立问题。
点评:中档题,不等式恒成立问题,往往要转化成求函数的最值,得到新的不等式进一步求解。本题主要考查学生的分析问题解决问题的能力。

练习册系列答案
相关题目
不等式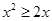 的解集是( ).
的解集是( ).
A.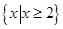 | B.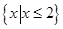 | C.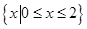 | D.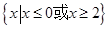 |
已知实数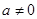 ,函数
,函数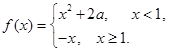 若
若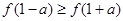 ,则实数
,则实数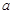 的取值范围是( )
的取值范围是( )
A.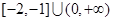 | B.[-2,-1] |
C.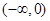 | D. |
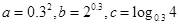 ,则
,则 从小到大的顺序是_____
从小到大的顺序是_____ ,
, ,
, .
.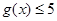 时,恒有
时,恒有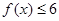 ,求
,求 的最大值;
的最大值; 时,恒有
时,恒有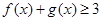 ,求
,求 、
、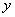 是不全为零的实数,试比较
是不全为零的实数,试比较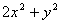 与
与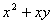 的大小;
的大小;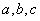 为正数,且
为正数,且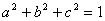 ,求证:
,求证: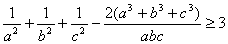 .
.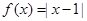 .
.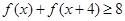 ;
;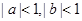 ,且
,且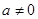 ,求证:
,求证: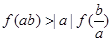 .
.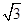 的一个近似值,令
的一个近似值,令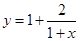 .
.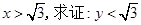 ;
; 都是正数,且
都是正数,且