题目内容
已知函数 ,
, ,
, .
.
(1)若当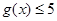 时,恒有
时,恒有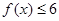 ,求
,求 的最大值;
的最大值;
(2)若当 时,恒有
时,恒有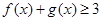 ,求
,求 的取值范围.
的取值范围.
(1)1;(2)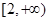 .
.
解析试题分析:本题考查绝对值不等式的解法、恒成立问题、不等式的性质等基础知识,考查学生运用函数零点分类讨论的解题思想和转化思想.第一问,先解绝对值不等式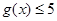 ,再解绝对值不等式
,再解绝对值不等式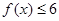 ,根据恒成立得两个集合的子集关系,求出a的取值范围;第二问,利用不等式的性质求出
,根据恒成立得两个集合的子集关系,求出a的取值范围;第二问,利用不等式的性质求出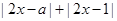 的最小值,再解绝对值不等式,求出a的取值范围.
的最小值,再解绝对值不等式,求出a的取值范围.
试题解析:(1)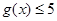
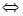
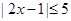
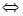
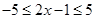
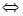
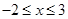 ;
;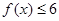
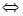
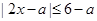
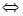
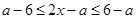
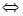
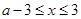 .
.
依题意有,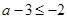 ,
,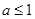 .
.
故 的最大值为1. 6分
的最大值为1. 6分
(2)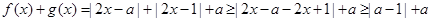 ,
,
当且仅当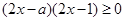 时等号成立.
时等号成立.
解不等式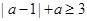 ,得
,得 的取值范围是
的取值范围是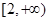 . 10分
. 10分
考点:1.绝对值不等式的解法;2.不等式的性质;3.恒成立问题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知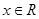 ,则“
,则“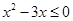 ”是“
”是“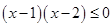 成立”的( )
成立”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
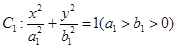 和
和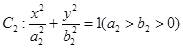 是焦点相同且
是焦点相同且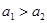 的两个椭圆,有以下几个命题:①
的两个椭圆,有以下几个命题:①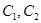 一定没有公共点;②
一定没有公共点;②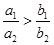 ;③
;③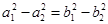 ;④
;④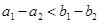 ,其中,所有真命题的序号为 。
,其中,所有真命题的序号为 。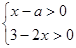 的整数解6个,则a的取值范围是____________.
的整数解6个,则a的取值范围是____________.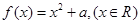 .
. ,比较
,比较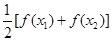 与
与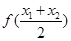 的大小;
的大小;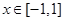 时,有
时,有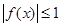 ,求实数
,求实数 的取值范围.
的取值范围.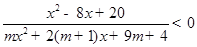 的解集为
的解集为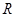 ,求实数
,求实数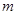 的取值范围。
的取值范围。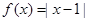
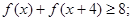
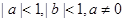 .求证:
.求证: .
.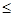
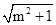 恒成立;命题q:方程x2+ax+2=0在实数集内没有解;若p和q都是真命题,求a的取值范围.
恒成立;命题q:方程x2+ax+2=0在实数集内没有解;若p和q都是真命题,求a的取值范围.