题目内容
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中，直线
的参数方程为
（
为参数），以原点
为极点，
轴的正半轴为极轴建立极坐标系，圆
上有一点
，且点，的极坐标分别为
，
.
（1）求圆的直角坐标方程及直线的普通方程；
（2）设直线与坐标轴的两个交点分别为
，
，点
在圆上运动，求
面积的最大值.
【答案】（1）圆
的直角坐标方程为
.直线
的普通方程为
.（2）
【解析】
（1）先将极坐标化为直角坐标，再根据标准式的圆方程，消去参数可得直线普通方程，（2）根据圆的性质可得圆上点到直线的距离的最大值即为圆心到直线的距离与半径之和，再根据面积公式得结果.
解：（1）因为点
的直角坐标为
，
圆心的直角坐标为
，
所以圆的半径
，
所以圆的直角坐标方程为
.
由直线的参数方程
，消去参数
，得
，
故直线的普通方程为.
（2）在直线：中，
令
，得
；令
，得
，
所以不妨设
，
，所以
.
又圆上点到直线的距离的最大值即为圆心
到直线的距离与半径之和，
设圆心到直线的距离为
，
所以
，
所以圆上的点到直线的距离的最大值为
，
所以
面积的最大值为
.
【题目】某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在
内,发布成绩使用等级制各等级划分标准见下表,规定： 
、
、
三级为合格等级, 
为不合格等级.
百分制 |
|
|
|
|
等级 |
|
|
|
|
为了解该校高一年级学生身体素质情况,从中抽取了
名学生的原始成绩作为样本进行统计,按照
的分组作出频率分布直方图如图
所示,样本中分数在
分及以上的所有数据的茎叶图如图
所示.
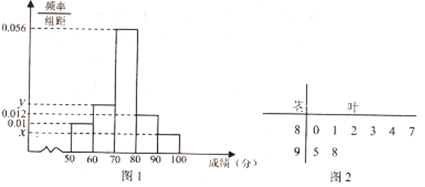
（1）求
和频率分布直方图中的
的值；
（2）根据样本估计总体的思想，以事件发生的频率作为相应事件发生的概率，若在该校高一学生任选
人,求至少有
人成绩是合格等级的概率；
（3）在选取的样本中,从
、
两个等级的学生中随机抽取了
名学生进行调研,记
表示所抽取的
名学生中为
等级的学生人数,求随机变量
的分布列及数学期望.
【题目】某人有楼房一幢，室内总面积为
，拟分割成两类房间作为旅游客房，有关的数据如下表：
大房间 | 小房间 | |
每间的面积 |
|
|
每间装修费 |
| 6000元 |
每天每间住人数 | 5人 | 3人 |
每天每人住宿费 | 80元 | 100元 |
如果他只能筹款80000元用于装修，且游客能住满客房，他应隔出大房间和小房间各多少间，能获得的住宿总收入最多？每天获得的住宿总收入最多是多少？
