题目内容
【题目】已知函数f(x)=ax-3lnx(a为常数)与函数g(x)=![]() -xlnx在x=1处的切线互相平行.
-xlnx在x=1处的切线互相平行.
(1)求a的值;
(2)求函数y=f(x)在[1,2]上的最大值和最小值.
【答案】(1)a=2(2)最小值为3-3ln![]() ;最大值为2
;最大值为2
【解析】
(1)由导数的几何意义可得f′(1)=g′(1),再求解即可;
(2)先利用导数研究函数数y=f(x)在[1,2]的单调性,然后求最值即可得解.
解:(1)f′(x)=a-![]() (x>0),g′(x)=-(lnx+1),由已知有f′(1)=g′(1),
(x>0),g′(x)=-(lnx+1),由已知有f′(1)=g′(1),
即![]() ,解得a=2.
,解得a=2.
(2)由(1)得:f(x)=2x-3lnx.
令f′(x)=2-![]() =0,解得x=
=0,解得x=![]() ,
,
∴当x∈(1,![]() )时,f′(x)<0,f(x)单调递减;
)时,f′(x)<0,f(x)单调递减;
当x∈(![]() ,2)时,f′(x)>0,f(x)单调递增.
,2)时,f′(x)>0,f(x)单调递增.
又f(1)=2,f(2)=4-3ln2,f(2)-f(1)=2-3ln2=ln![]() <0.
<0.
∴函数f(x)在[1,2]上的最小值为f(![]() )=3-3ln
)=3-3ln![]() ,最大值为f(1)=2,
,最大值为f(1)=2,
故函数f(x)在[1,2]上的最小值为3-3ln![]() ,最大值为2.
,最大值为2.

【题目】影响消费水平的原因很多,其中重要的一项是工资收入.研究这两个变量的关系的一个方法是通过随机抽样的方法,在一定范围内收集被调查者的工资收入和他们的消费状况.下面的数据是某机构收集的某一年内上海、江苏、浙江、安徽、福建五个地区的职工平均工资与城镇居民消费水平(单位:万元).
地区 | 上海 | 江苏 | 浙江 | 安徽 | 福建 |
职工平均工资 | 9.8 | 6.9 | 6.4 | 6.2 | 5.6 |
城镇居民消费水平 | 6.6 | 4.6 | 4.4 | 3.9 | 3.8 |
(1)利用江苏、浙江、安徽三个地区的职工平均工资和他们的消费水平,求出线性回归方程![]() ,其中
,其中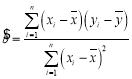
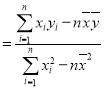 ,
,![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1万,则认为得到的线性回归方程是可靠的,试问所得的线性回归方程是否可靠?(![]() 的结果保留两位小数)
的结果保留两位小数)
(参考数据:![]() ,
,![]() )
)